基本介紹
- 中文名：正則方程
- 外文名：canonical equations
- 相關函式：哈密頓函式
- 所屬學科：數學
- 提出者：W.R.哈密頓
- 別稱：哈密頓正則方程
方程簡介,力法正則方程,
方程簡介
（1）式中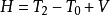
，稱為哈密頓函式，T2和T0分別為動能T中用廣義坐標表示的二次齊次式和零次齊次式（即不含p，僅含q和t之式），V為用廣義坐標表示的勢能函式。
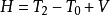
對於定常系統
，
，則H=T+V，即這種力學系統的哈密頓函式就是這系統用廣義動量和廣義坐標表示的機械能。
由於H函式須將T中的q換成p，所以求正則方程要比求拉格朗日方程多一層運算手續。正則方程是2N個一階微分方程組；拉格朗日方程是N個2階微分方程組。正則方程形式上的優點是每一式只有一個導數，而且在式（1）的左邊，右邊是q，p，t的函式。若令
，
，…，
；
，
，…，
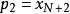，則式（1）可寫成：
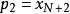
這種微分方程在數學中有系統的研究。
力法正則方程
以多餘約束力作為基本未知量、由變形諧調條件建立補充方程求解超靜定問題的方法稱為力法。
用力法求解超靜定系統需遵循以下步驟：①判斷多餘約束的個數，即確定超靜定的階數；②解除所有的多餘約束選擇原超靜定結構的一個靜定基；③施加外載荷和多餘約束力以及對應的約束條件，形成一個相當系統；④在相當系統上列出求解約束位移的補充方程(組)，補充方程中包含有未知的多餘約束力；⑤求解補充方程中的未知數即多餘約束力。
從上述求解步驟可以看出，在相當系統上列出包含有未知多餘約束力的補充方程(組)是一個關鍵環節。在解除多餘約束代之以多餘約束的同時，多餘約束在其作用點對超靜定系統的位移的限制與多餘約束力的作用方向正好相反(如限制向下的線位移則多餘約束力向上、限制逆針向轉動的約束力偶必須順針向等)，也就是說，多餘約束與對應的約束位移之間一定是一對廣義力與廣義位移的關係，由此可以得到求解超靜定問題的正則方程。
設一個n階超靜定結構的n個多餘約束力為Xi，(i=1~n)，對應的約束位移為Δi。在相當系統上還有外載荷，外載荷在Xi作用點引起的與Xi對應的廣義位移為ΔiF，多餘約束力Xj在Xi作用點引起的廣義位移為Δij，根據位移疊加法
因為Δij是Xj單獨作用在相當系統引起的，所以與Xj成正比，設Xj=1（單位力）引起的Δij為δij，即Δij=Xjδij，上式可寫成
上式用矩陣形式可寫為
或寫成更簡捷的形式
