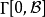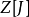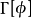基本介紹
- 中文名:背景場方法
- 外文名:Background field method
- 領域:量子力學
原理,套用,
原理







如果將 寫成經典場
寫成經典場 (稱為背景場)和量子場
(稱為背景場)和量子場 的疊加:
的疊加:








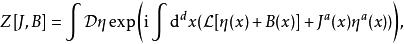

對 的路徑積分表達式作
的路徑積分表達式作 的變數代換,可以證明:
的變數代換,可以證明: ,特別地,
,特別地,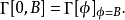



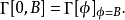
因此,為計算量子場 的有效作用量
的有效作用量 ,只需計算
,只需計算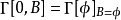 ,後者通常會使用微擾方法計算:將作用量
,後者通常會使用微擾方法計算:將作用量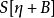 中
中 的二次項當作無擾的作用量,用以構建
的二次項當作無擾的作用量,用以構建 場的傳播子,包含
場的傳播子,包含 更高階次的項則視為相互作用項,並以微擾展開的方法處理。在這種處理下,
更高階次的項則視為相互作用項,並以微擾展開的方法處理。在這種處理下, 是背景場存在時,所有單粒子不可約的真空圖的貢獻之和。量子場只出現在這些圖的內線中,而背景場只出現在這些圖的外線中。進行重整化時,背景場的場強需要重整化,但量子場的場強不需要重整化。
是背景場存在時,所有單粒子不可約的真空圖的貢獻之和。量子場只出現在這些圖的內線中,而背景場只出現在這些圖的外線中。進行重整化時,背景場的場強需要重整化,但量子場的場強不需要重整化。


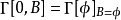
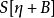




套用
背景場方法常被用於規範場的量子化。描述規範場論時,通常會從一個規範對稱的作用量出發。然而為了量子化規範場,需要向作用量中引入規範固定項(和鬼場,對於非阿貝爾規範場),如下所示:


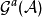

規範固定後的作用量失去了原有的規範對稱性。選取特定的規範並不會對可觀測量的計算帶來影響,這些量仍然具有規範對稱性。但是不可觀測的量,如格林函式、有效作用量以及重整化時引入的抵消項,通常不再具有規範對稱性。
如果使用背景場方法,在規範場上疊加一個經典場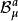 ,並選取如下的規範固定項(這種規範也被稱為背景場規範):
,並選取如下的規範固定項(這種規範也被稱為背景場規範):
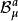
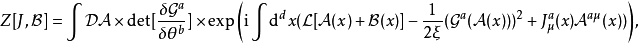

那么生成泛函 在如下的無窮小規範變換下保持不變:
在如下的無窮小規範變換下保持不變: