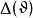重整化步驟通常用格林函式來表述。和S矩陣不一樣,格林函式不是規範不變的對象,它們的值依賴於所選擇的特殊的規範條件。相對性原理等效於在格林函式之間存在著一些關係;類比於電動力學,我們稱這種關係為廣義瓦德恆等式。
基本介紹
- 中文名:瓦德恆等式
- 外文名:Ward identities
- 定義:不同規範的物理等效性
- 套用學科:量子力學術語
- 範疇:數理科學
- 涉及:格林函式
概念,基本原理,
概念
重整化步驟通常用格林函式來表述。和S矩陣不一樣,格林函式不是規範不變的對象,它們的值依賴於所選擇的特殊的規範條件。相對性原理等效於在格林函式之間存在著一些關係;類比於電動力學,我們稱這種關係為廣義瓦德恆等式。這種關係提供了不同規範的物理等效性,並在證明重整化S矩陣的規範不變性和么正性時起關鍵作用。特別是,由它們可知,為消除去掉中間正規化後出現的發散所需要的抵消項有規範不變的結構。
基本原理
我們先對正規化的未重整格林函式推導廣義瓦德恆等式。在所有以下的論證中,所需要用的只是正規化作用量的規範不變性。
作為格林函式生成泛函式的原始表示,可以選用:

讓我們引進用以下條件定義的規範不變函式 :
:













考慮到泛函 在表面
在表面 上的值等於泛函
上的值等於泛函 在表面
在表面 上的值,我們得到:
上的值,我們得到: