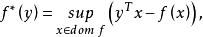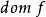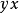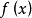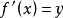共軛函式亦稱對偶函式、極化函式,函式的某種對偶變換。設f為實線性空間X上的擴充實值函式,X*為X的某個對偶空間,即由X上的一些線性函式所構成的實空間,那么f的共軛函式f*是X*上的擴充實值函式。共軛函式的概念在研究極值問題的對偶理論中起著本質作用。19世紀,法國數學家勒讓德首先在力學中引進類似的概念,那是把速度變為動量的變換,對於力學方程來說,這就使得拉格朗日方程變為哈密頓方程。今天,人們就稱這樣的變換為勒讓德變換,勒讓德變換的概念實際上出現得比對偶空間或共軛空間的概念還要早,應該說,後一概念的起源之一就是勒讓德變換。20世紀50年代,芬切爾又把勒讓德變換進一步抽象為共軛函式的概念,因此,今天人們又把函式到其共軛函式的變換稱為勒讓德-芬切爾變換。
基本介紹
- 中文名:共軛函式
- 外文名:conjugate function
- 別名:對偶函式、極化函式
- 相關人物:勒讓德、芬切爾等
- 相關概念:勒讓德變換、對偶變換等
定義,基本性質,舉例分析,仿射函式,負對數函式,指數函式,負熵函式,反函式,
定義
設函式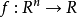 ,定義函式
,定義函式 為
為
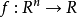

 圖1
圖1顯而易見,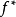 是凸函式,這是因為它是一系列
是凸函式,這是因為它是一系列 的凸函式(實質上是仿射函式)的逐點上確界。無論f是否是凸函式,
的凸函式(實質上是仿射函式)的逐點上確界。無論f是否是凸函式,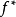 都是凸函式。(注意到這裡當
都是凸函式。(注意到這裡當 是凸函式時,下標
是凸函式時,下標 可以去掉,這是因為根據關於擴展值延伸的定義,對於
可以去掉,這是因為根據關於擴展值延伸的定義,對於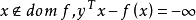 )。
)。
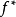

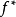


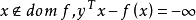
基本性質
Fenchel不等式
從共軛函式的定義我們可以得到,對任意 和
和 ,如下不等式成立
,如下不等式成立




以函式 為例,其中
為例,其中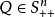 ,我們可以得到如下不等式
,我們可以得到如下不等式

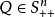

共軛的共軛
可微函式
可微函式f的共軛函式亦稱為函式f的Legendre變換。(為了區分一般情況和可微情況下所定義的共軛,一般函式的共軛有時稱為Fenchel共軛。)
設函式f是凸函式且可微,其定義域為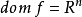 ,使
,使 取最大的
取最大的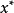 滿足
滿足 ,反之,若
,反之,若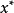 滿足
滿足 ,
, 在
在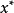 處取最大值。因此,如果
處取最大值。因此,如果 ,我們有
,我們有
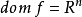

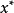

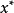


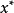




我們亦可以換一個角度理解。任選 ,令
,令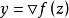 ,則
,則

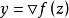

伸縮變換和複合仿射變換
若a>0以及b∈R, 的共軛函式為
的共軛函式為 。
。


設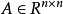 非奇異,
非奇異, ,則函式
,則函式 的共軛函式為
的共軛函式為
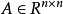




獨立函式的和
如果函式 ,其中
,其中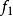 和
和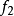 是凸函式,且共軛函式分別為
是凸函式,且共軛函式分別為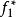 和
和 ,則
,則

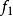
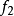
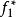


舉例分析
考慮R上一些凸函式的共軛函式。
仿射函式

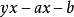
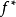


負對數函式
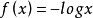




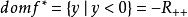
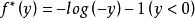
指數函式


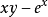
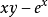




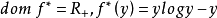
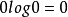
負熵函式
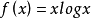





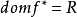


反函式