勒壤得轉換

勒壤得轉換（英語：Legendre transformation）是一個在數學和物理中常見的技巧，得名於阿德里安-馬里·勒壤得（Arien-Marie Legendre）。該操作是一個實變數的實值凸函式的對合變換。 它經常用於經典力學中，從拉格朗日形式導出哈密頓形式；以及在熱力學中，推導出熱力學勢，並求解多個變數的微分方程。

基本介紹

• 中文名：勒壤得轉換
• 外文名：Legendre transformation
• 學科：數學

定義

更詳細地定義勒壤得轉換，為了求得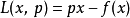關於x的最大值，設定關於x的偏導數為零：

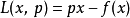
則

。(1)

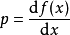
這表達式必為最大值。因為，凸函式 的二階導數是負數：

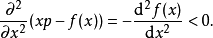
用方程 (1) 來計算函式f的反函式x=g(p)。代入L(x,p) 方程，即可以得到想要的形式：。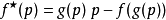

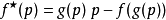
計算f(x) 的勒壤得轉換，所需的步驟為：

（1）找出導函式，

（2）計算導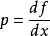函式 的反函式 ，

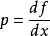
（3）代入 F(x)方程來求得新函式 。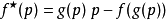

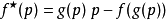
這定義切確地闡明：勒壤得轉換製造出一個新函式 ；其新自變數為 。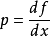

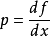
數學性質

以下討論，函式f的勒壤得轉換皆標記為。

標度性質

勒壤得轉換有以下這些標度性質：

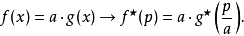
由此可知，一個 r 次齊次函式的勒壤得轉換是一個s次齊次函式；這裡，。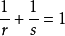

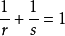
平移性質

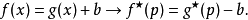
反演性質

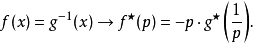
線形變換性質

讓 A 成為一個從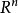到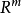的線形變換。對於任何定義域為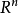的凸函式 f ，必有

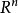
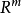
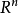
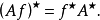
這裡，是 A 的伴隨運算元定義為

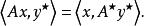
套用

熱力學

在熱力學里，使用勒壤得轉換主要的目的是，將一個函式與所含有的一個自變數，轉換為一個新函式與所含有的一個新自變數，（此新自變數是舊函式對於舊自變數的偏導數）；將舊函式減去新自變數與舊自變數的乘積，得到的差就是新函式。勒壤得轉換可以用來在各種熱力勢（thermodynamic potential）之間作轉換。

經典力學

在經典力學里，勒壤得轉換專門用來從拉格朗日表述導引出哈密頓表述，或反導之

正則變換

正則變換廣泛地套用勒壤得轉換在其理論里。

參閱

• 哈密頓力學
  
• 切觸幾何
  
• 正則變換