基本介紹
- 中文名:切觸幾何
- 外文名:contact geometry
- 研究:流形上的完全不可積超平面的幾何
- 根源:出現於克里斯蒂安·惠更斯著作中
- 簡介:奇數維流形上的一種幾何結構
- 相關術語:弗洛比尼斯定理
歷史
定義
Reeb向量場
形式和結構

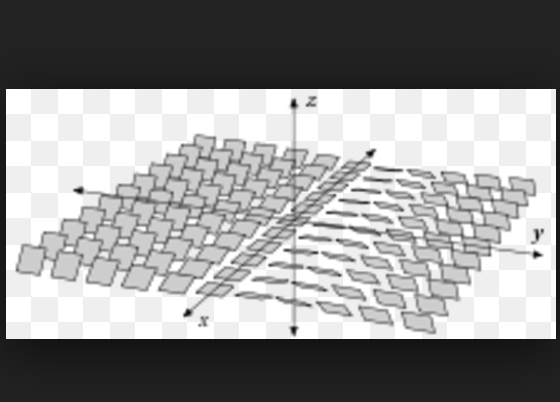

數學上,切觸幾何(英語:Contact geometry)是研究流形上的完全不可積超平面的幾何。根據弗洛比尼斯定理,這個(大致來講)可以通過葉狀結構的不成立來識別。作為它的姐妹,辛幾何屬於偶數維的世界,而切觸幾何是奇數維...
三維流形上的tight切觸結構的存在性和分類是三維切觸幾何中的一個基本問題。 在本項目中,我們主要研究帶一個環面邊界的小的Seifert流形上的tight切觸結構的分類和雙曲的有理同調球上的tight切觸結構的存在性。這將對認識圖流形上的tight...
overtwisted切觸三維流形中的non-loose Legendrian紐結的存在性, 以及open book分解的分數的Dehn twist係數的估計,切觸三維流形的支撐虧格的計算. 這些問題的研究和解決將加深人們對切觸三維流形的拓撲,幾何,特別是它們的各種不變數,的...
包括以下幾個方面:1.研究AdS空間中的平坦類時子流形的幾何性質,對平坦類時曲面的奇點進行分類並研究其與某些模型曲面(全臍子流形)之間的切觸關係;2.利用形變理論和開折理論研究AdS空間中的子流形與該空間的測地線的切觸關係,...
本項目的研究成果有望有效地推動接觸幾何和變分理論的發展,有重要的理論價值。結題摘要 我們改進了A.Bahri 在他1996的專著中所定義的一個擬梯度流。這個擬梯度流定義在三維緊切觸流形的對偶Legendrian曲線的一個子空間上。我們還研究了...
而當滿足條件(3>時,則M是較具保圓型結構的仿切觸黎曼流形廣泛的一類EP佐佐木流形,且稱之為LP佐佐木流形.佐佐木流形和P佐佐木流形與其他流形一樣,從它引進以來便有豐富多彩的微分幾何與拓撲學的問題可供研究.有關的論述已由國內外...
流形與子流形的結構和性質及分類是現代幾何研究的重要任務之一。葉狀流形是一種具有特殊結構的流形,研究這種流形有著十分重要的理論意義和廣泛的套用前景,如了解葉狀信息流形,微分方程解的葉狀對稱性質,葉狀辛結構、切觸結構、芬斯勒結構...
本項目取得了三個方面的研究成果:一是研究了平面上四階常微分方程的幾何,發現該方程在切觸變換下的不變數;研究具球面曲率線曲面的模空間;研究3維空間中保主曲率曲面的等距形變。二是研究子流形的幾何;建立了DesItter空間中緊緻類空...
還研究了球型四元切觸流形上的幾何與分析,構造了共形不變數,提出了qc正質量猜想,並套用於Sp(n + 1, 1)的凸余緊子群。把多複變函數論中關於復Monge-Ampere運算元的多重位勢理論推廣到 k-Hessian運算元及四元Monge-Ampere運算元:定義...
古希臘數學家梅內克繆斯(Menaechmus)的解題、證明方式與現在使用坐標系十分相似,以至於有時會認為他是解析幾何的鼻祖。阿波羅尼奧斯在《論切觸》中解題方式在現在被稱之為單維解析幾何;他使用直線來求得一點與其它點之間的比例。阿波羅...
.在本項目中我們將利用構造性代數幾何的觀點、理論和方法研究處理多元有理插值問題,包括多元Cauchy型有理插值和多元切觸有理插值解的存在性及其表示;流形上的有理插值問題及其在密碼學中的套用,以及相應的高效快速算法的構造;研究由插值...
面積、曲線的長等問題.第13講是與前面沒多大關係的內容—關於方程的幾何作圖法.巴羅的講義通篇採用古典的幾何觀點來處理切線問題和求積問題,而不是像沃利斯那樣採取分析的方法.例如他把曲線的切線定義為同曲線僅在一點切觸的直線.但他...
伴隨著此領域內的一些重要結果越來越多,時至今日近切觸幾何逐漸成為微分幾何里最熱門的研究分支之一。本項目將此類流形作為主要研究對象,藉助張量分析和幾何分析方法深入討論它們的幾何結構和拓撲性質。 本項目的主要研究結果是近Kenmots...
阿波羅尼奧斯(古希臘語:Ἀπολλώνιος)(約前262年至前190年),又譯為阿波羅尼烏斯,阿波羅尼等,生於小亞細亞南岸的佩爾加,古希臘幾何學家。著有《圓錐曲線論》八卷,《論切觸》(Ἐπαφαί)等。 在他的八卷本...
擬Hermitian幾何與次黎曼幾何、切觸幾何、Hermitian幾何等等有著密切的聯繫。擬調和映射是水平能量泛函的臨界點。項目利用擬調和熱流的方法得到了擬調和映射的Eells-Sampson型存在性結果和Hartman型唯一性結果。項目還研究了擬Hermitian流形上的...
本書還特彆強調了辛幾何和切觸幾何的套用。 作者的名著Partial Differential Relations是面向專家的關於h-原理的百科全書,而本書則是第一本關於此理論及其套用的能被廣泛接受的論著。本書是關於解偏微分等式和不等式幾何方法的一本很好...
王佳 王佳 Sasaki空間型的M(C)切觸-子流形 數學季刊 第4卷第1期 46-51 其它 王佳 王佳 具有常曲率的芬斯勒空間 西南師範大學學報(自然科學版) 第30卷第5期 792-795 其它 王佳 王佳 關於一類特殊的射流 西南師範大學學報(自然...
法諾主要從事n維空間的射影幾何與代數幾何研究,對直線幾何、有限幾何、代數曲面、流形、雙有理切觸變換、非歐幾何及有理係數線性微分方程等有關論述,證明了三維空間中存在無理對合等結果。法諾寫過許多教科書,著有《不可約張量集》(...
