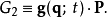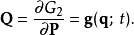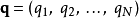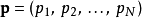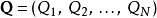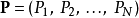正則變換生成函式

在哈密頓力學里，當計算正則變換時，生成函式扮演的角色，好似在兩組正則坐標之間的一座橋。為了要保證正則變換的正確性 ，採取一種間接的方法，稱為生成函式方法。

基本介紹

• 中文名：正則變換生成函式
• 外文名：Regular transformation generated function
• 學科：哈密頓力學
• 領域：力學
• 相關術語：正則變換
• 類別：4類

簡介

在哈密頓力學里，當計算正則變換時，生成函式扮演的角色，好似在兩組正則坐標之間的一座橋。為了要保證正則變換的正確性 ，採取一種間接的方法，稱為生成函式方法。這兩組變數必須符合方程

；(1)

其中， 是舊廣義坐標， 是舊廣義動量， 是新廣義坐標， 是新廣義動量， 分別為舊哈密頓量與新哈密頓量。

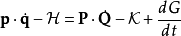
生成函式 G 的參數，除了時間以外，一半是舊的正則坐標；另一半是新的正則坐標。視選擇出來不同的變數而定，一共有四種基本的生成函式。每一種基本生成函式設定一種不同的變換，從舊的一組正則坐標變換為新的一組正則坐標。這變換 保證是正則變換。

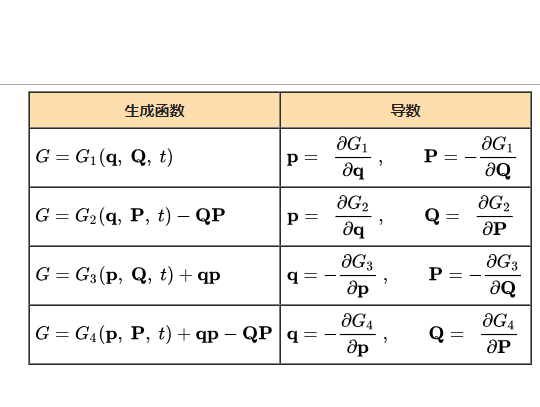
生成函式列表

生成函式	導數

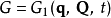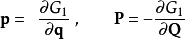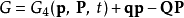生成函式

第一型生成函式

第一型生成函式G₁只跟舊廣義坐標、新廣義坐標有關，

代入方程 (1) 。展開生成函式對於時間的全導數，

新廣義坐標Q和舊廣義坐標q都是自變數，其對於時間的全導數 互相無關，所以，以下 2N+1 個方程都必須成立：

，(2)

，(3)

。(4)

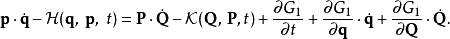
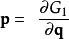
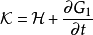
這 2N+1個方程設定了變換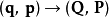 ，步驟如下：

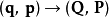
第一組的N個方程 (2) ，設定了P的N個函式方程 。

在理想情況下，這些方程可以逆算出Q的N個函式方程

。(5)

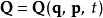
第二組的N個方程 (3) ，設定了P的N個函式方程 。

代入函式方程 (5) ，可以算出P的N個函式方程

。(6)

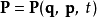
從2N個函式方程 (5) 、(6) ，可以逆算出2N個函式方程

， 。

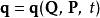
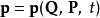
代入新哈密頓量K的方程 (4) ，可以得到 。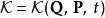

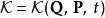
第二型生成函式

第二型生成函式G₂只跟舊廣義坐標q、新廣義動量P有關 ：

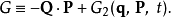
代入方程 (1) 。展開生成函式隨時間的全導數：

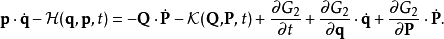
由於舊廣義坐標q 與新廣義動量P必須彼此無關，以下 2N+1方程必須成立：

，(7)

，(8)

。(9)

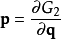
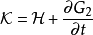
這 2N+1個方程設定了變換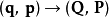 。步驟如下：

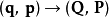
第一組的N個方程 (7) ，設定了p的函式方程 。

在理想情況下，這些方程可以逆算出P的函式方程

。(10)

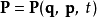
第二組的N個方程 (8) ，設定了的函式方程 。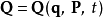

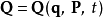
代入函式方程 (10) ，可以算出Q函式方程

。(11)

由函式方程 (10) 、(11) ，可以算出函式方程 ， 。

代入新哈密頓量的方程 (9) ，則可得到 。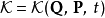

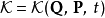
第三型生成函式

第三型生成函式只跟舊廣義動量p、新廣義坐標Q有關：

以下2N+1方程設定了變換 ：

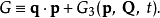
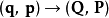
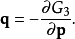
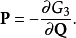
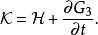
第四型生成函式

第四型生成函式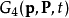 只跟舊廣義動量p、新廣義動量P有關：

以下 2N+1方程設定了變換 ：

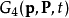
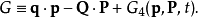
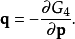
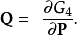
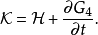
示例

實例 1

第一型生成函式有一個特別簡易案例：

方程 (2) ，(3) ，(4) 的答案分別為

實例 2

再舉一個涉及第二型生成函式，比較複雜的例子。讓

這裡，g是一組N 個函式。答案是一個廣義坐標的點變換，