極小理想

極小理想是一類特殊理想，是與極大理想相對偶的概念。

環R的一個左(右)理想a，若a不真含R的非零左(右)理想，則稱a為R的極小左(右)理想。類似地，可定義極小理想。極小理想在本原環理論中有重要作用。

基本介紹

• 中文名：極小理想
• 外文名：minimal ideal
• 適用範圍：數理科學

定義

若環 R 的（左，右）理想 I 滿足：

① R 真包含 I ；

② 真包含 I 的（左，右）理想只有 R，則稱 I 為 R 的極大 [左，右] 理想(maximal [left,right] ideal)。

若環 R 的（左，右）理想 I 滿足：

1）零理想真包含於 I；

2）真包含於 I 的（左，右）理想只有零理想，則稱 I 為 R 的極小 [左，右]理想 (minimal [left,right] ideal)。

理想

[ideal]

若環 R 的非空子集 S 關於 R中的加法和乘法封閉，即 ，則 S 本身關於此加法和乘法成為一個環，稱為 R 的一個子環(subring)，環R的子集 為 R 的一個子環，稱為環 R 的中心(center ofa ring)，記作 Z(R)。

左右理想

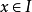設 I 為環 R 的子環，若對任意的 及 都有 ，則稱 I 為 R 的一個左理想(left ideal)。若對任意的及 都有 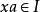，則稱 I 為 R 的一個右理想(right ideal) 。若 I 既是左理想又是右理想，則稱 I 為 R 的一個(雙邊) 理想。環 R 的只含零元的子集為 R 的一個理想，稱為零理想(zero ideal)，記作 0 。環 R 本身也是 R 的一個理想，稱為單位理想(unit ideal)。

理想的和積

若 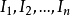為環 R 的理想，則集合 仍為 R 的理想，稱為理想的和(sum of ideals)，記作 。所有形如 (其中 ) 的元素的有限和的集合亦為R的理想，稱為理想 的積(product of ideals)，記作。

理想環

若 X 為環 R 的子集，則 R 的包含 X 的所有子環(左理想、右理想、理想) 的交稱為由 X 生成的 R 的子環(左理想、右理想、理想) (subring (left ideal,right ideal,ideal) generatedby X)。由一個元素生成的左理想(右理想、理想) 稱為主左理想(主右理想、主理想) [principal left ideal (principal right ideal,principal idea)]。若環R 中的每個左(右) 理想都是主左(右) 理想，則稱R 為主左(右) 理想環[principalleft (right) ideal ring]。

若 I 為環 R 的理想，則加法商群 關於乘法成為一個環，稱為環 R 模理想 I 的剩餘類環 (residue class ring) 或商環 (quotient ring,factor ring)。若 為環 R 的兩個理想，則加法商群 為商環的理想，稱為理想 J與 I 的商 (quotient of ideals)。