基本介紹
- 中文名:局部環
- 外文名:Stellenringe
- 領域:數學
定義
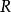
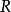
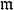
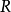
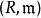
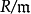
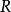
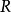
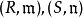
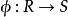
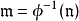
例子
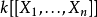
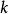
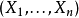
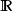
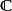
動機與幾何詮釋
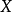
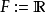
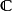
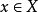
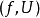
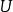

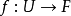
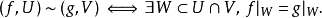






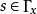
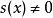

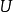
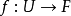
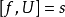
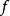
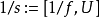
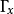

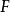
非交換的情形
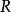
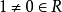
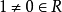
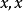
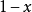
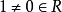
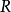
- R 的唯一極大左理想。
- R 的唯一極大右理想。
- R 的Jacobson根。
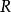
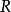
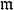
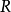
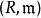
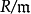
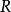
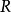
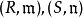
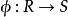
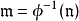
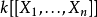
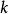
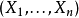
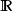
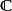
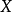
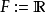
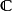
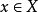
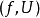
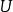

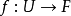
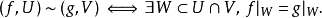






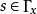
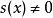

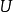
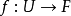
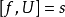
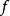
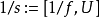
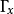

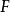
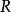
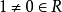
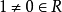
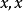
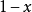
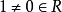
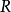
在數學中,局部環是只有一個極大理想的交換含麼環。局部環的概念由 Wolfgang Krull 於1938年引入,稱之為Stellenringe,英譯 local ring 源自扎里斯基。...
地形的差異,造成地表熱力性質的不均勻性,往往形成局部環流。最常見的有:山谷風、海陸風(水陸風)、城市“熱島”效應等。 ...
正則局部環是局部環的子類,有正則參數系的局部環(R,m)稱為正則局部環,即m可由dimR個元素生成。...
電網局部環式運行指電網局部的每一點都能從一個或兩個電源沿兩條不同線路供電的運行方式。如果該電網中每一點正常都由兩條線路供電,則該運行方式稱“閉環”;...
局部化,是分式環的另一名稱,局部化有兩個重要性質,即保持正合性和諾特性質,通過哥爾迪(Goldie,A. W.)等人的工作,局部化方法已套用於非交換環論研究中.例如,...
局部代數(local algebra)是與局部環相應的一類特殊代數。菲廷(Fitting,H.)證明了:若A模N的自同態代數EndA(N)是局部的,則N不可分解。當A是域F上有限維代數時...
半完全環是介於完全環與半局部環之間的一類環。設J(R)是環R的雅各布森根,若R/J (R)是半單環,且R/J (R)的冪等元可提升為R的冪等元,則稱R為半完全...
賦值環(valuation ring)是一種特殊的局部環。也是重要的交換環類。交換環R稱為賦值環。賦值環是交換的特殊序列。它與戴德金環有密切的關係。事實上,交換諾特局部...
在交換代數中,科恩-麥考利環是對應到一類代數幾何性質(例如局部等維性)的交換環。... 正則局部環皆為Cohen-Macaulay 環。 Gorenstein環皆為 Cohen-Macaulay,其中...
環空間((ringed space)一類重要的拓撲空間.指一種帶有一個環層Ox的拓撲空間X.環層Ox被稱為環空間(X,Ox)的結構層一般地,Ox是一個帶單位元的交換環層.環...
諾特概形(Noetherian scheme)是諾特環的推廣。若一個概形X有一個由諾特環的譜所構成的有限仿射開覆蓋,則稱X是諾特概形。概形是代數幾何的基本研究對象。它實際...
有限階賦值環(valuation ring of finite rank)是賦值環的特殊類。具有有限個非零真素理想的賦值環,稱為有限階賦值環。只有一個非零真素理想的賦值環稱為一階...
《內容包括Groebner基理論,解多項式方程組的算法,結式理論,局部環計算理論,模與同調的計算理論,多面體幾何計算理論,在整數規劃與組合數學中的套用。在代數編碼理論中...
在抽象代數中,交換代數旨在探討交換環及其理想,以及交換環上的模。代數數論與代數幾何皆奠基於交換代數。交換環中最突出的例子包括多項式環、代數整數環與p進數環,...
在交換代數中,一個葛侖斯坦環(英文:Gorenstein ring)是對每個素理想的局部化皆為葛侖斯坦局部環的交換環。...
另外,還討論了離散賦值環、CohenMacaulay 環和正則局部環。本書可作為本科生或研究生的交換代數和代數幾何課程的入門教材或參考書。...
正規賦值(canonical valuation)是由賦值建立賦值環的逆問題所決定的賦值。給定域F上的賦值環B,可建立F上的賦值φB,使得φB的賦值環為B,這樣的φB稱為B確定的...
設Z是余維r的閉子概型, 是Z的所有餘維r的不可約分支,定義 為相伴於Z的環元,其中 是Z在 的廣點 的局部環 的長度。設 為簇間的態射,Y為X的子簇....
概形是代數幾何的基本研究對象。它實際上就是一個局部同構於仿射概形的局部環空間。更精確地,概形(X,OX)是一個環空間,其拓撲空間X有一個開覆蓋{Xi}i∈I,...
正則參數系是用來刻畫正則局部環的概念。若(R,m)是克魯爾維數為 r的局部環,則m中存在r個元素,它們生成的理想是 m 準素理想,此時,(a1,a2, ... ,ar)稱...
線上性代數中,迪厄多內行列式是矩陣與除環和局部環上矩陣的行列式的推廣。 它是在1943年由迪厄多內提出的。...
