正則局部環是局部環的子類，有正則參數系的局部環(R,m)稱為正則局部環，即m可由dimR個元素生成。
基本介紹
- 中文名：正則局部環
- 外文名：regular local ring
- 適用範圍：數理科學
簡介,正則環,局部環,
簡介
正則局部環是局部環的子類，有正則參數系的局部環(R,m)稱為正則局部環，即m可由dimR個元素生成。
正則環
[regular ring]
設(R,m)是一個諾特局部環。假設R的維數為d，則m的生成元組所含元素的個數至少為d。如果m可以有d個元素生成，則稱 R 是正則局部環（regular local ring），此時，m的由d個元素組成的生成元組稱為是R的正則參數系（regular system of parameters）。
對一般的諾特環R，如果對任意素理想p，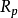
都是正則局部環，則稱R是正則環。
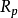
正則環一定是科恩-麥考萊的。正則環也一定是正規的。
例如，設F是域，則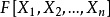
是正則環。
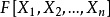
局部環
[local ring]
設R是一個環，如果R含有唯一的極大理想m，則稱R是局部環，記為(R,m)，有時也記為(R,m,k)，其中k=R/m是一個域。
注意到，若(R,m)是局部環，則m恰由R的所有非可逆元組成。
設𝖕是R的一個素理想，則R𝔭是局部環。
如果R含有有限多個極大理想，則稱R是一個半局部環（semi-local ring）。
