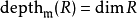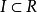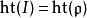科恩-麥考利環

在交換代數中，科恩-麥考利環是對應到一類代數幾何性質（例如局部等維性）的交換環。

基本介紹

• 中文名：科恩-麥考利環
• 外文名：Cohen-Macaulay ring
• 屬於：交換環
• 學科：交換代數
• 領域：交換代數
• 性質：純粹性

介紹

在交換代數中，Cohen-Macaulay環是對應到一類代數幾何性質（例如局部等維性）的交換環。

此概念依數學家弗朗西斯·索爾比·麥考利（Francis Sowerby Macaulay）與歐文·索爾·科恩（Irvin S. Cohen） 命名，麥考利（1916年）證明了多項式環的純粹性定理，科恩（1946年）則證明了冪級數環的情形；事實上所有Cohen-Macaulay環都具純粹性。

形式定義

若交換局部環滿足，其中 depth 表深度而 dim 表克魯爾維數，則稱之為Cohen-Macaulay環。此性質在局部化之下不變。

一般而言，若交換環R對所有素理想的局部化皆為Cohen-Macaulay環，則稱之為Cohen-Macaulay 環。

若一個概形的所有局部環皆為Cohen-Macaulay環，稱之為Cohen-Macaulay概形。

例子

• 正則局部環皆為 Cohen-Macaulay 環。
  
• Gorenstein環皆為 Cohen-Macaulay，其中重要的特例是完全交環。
  
• 有理奇點對應到 Cohen-Macaulay 環，卻不一定是 Gorenstein 環。
  
• 阿廷環皆為 Cohen-Macaulay 環。
  
• 設k為域，冪級數環k[t]的一維子環k[[t²,t⁵]]}並非正則環，而仍屬 Gorenstein 環。
  
• 承上，k[[t³,t⁴,t⁵]]}並非 Gorenstein 環，而仍屬 Cohen-Macaulay 環。
  
• 一般而言，任何一維的諾特整環都是 Cohen-Macaulay 環。
  

幾何詮釋

Cohen-Macaulay 條件的一種詮釋見諸凝聚對偶性，其中模的“對偶化對象”本屬於某個導範疇，當考慮的環是 Cohen-Macaulay 環時，該對象可由某個模代表。Gorenstein 條件則更精細，它斷言此對偶對象由可逆層代表。正則性最強，它對應於交換環譜在該點的平滑性。就幾何觀點，Gorenstein 與 Cohen-Macaulay 條件是平滑性的逐步推廣，在此框架下可以證明較廣的幾何定理。

純粹性定理

設R為諾特環，為其理想。若對每個R/I的相伴素理想皆有，則稱 I為純粹的。若每個能由個元素生成之理想I都是純粹的，則稱R滿足純粹性定理。一個諾特環R滿足純粹性定理若且唯若它是 Cohen-Macaulay 環。