可逆層是環空間上的一類結構層。當X是代數簇或解析空間時,可逆層與線叢之間有著一個一一對應的關係。此外可逆層與除子之間也有一個很好的對應關係,這使得可逆層成為代數幾何中的一個重要研究工具。
基本介紹
- 中文名:可逆層
- 外文名:invertible sheaf
- 適用範圍:數理科學
定義

相關概念




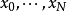
性質
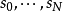
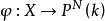
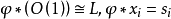
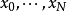
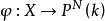
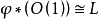
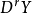

可逆層是環空間上的一類結構層。當X是代數簇或解析空間時,可逆層與線叢之間有著一個一一對應的關係。此外可逆層與除子之間也有一個很好的對應關係,這使得可逆層成為代數幾何中的一個重要研究工具。





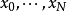
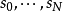
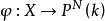
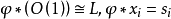
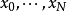
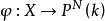
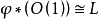
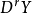
可逆層是環空間上的一類結構層。當X是代數簇或解析空間時,可逆層與線叢之間有著一個一一對應的關係。此外可逆層與除子之間也有一個很好的對應關係,這使得可逆層...
1 簡介 2 可逆層 豐富除子簡介 編輯 豐富除子H就是滿足Nakai判別法的除子:HC>0, HH>0, 這裡C是任何不可約曲線, HC是H與C的相交數, HH是H的自交數。...
豐富層((ample sheaf)與到射影空間內的嵌人有關的局部自由層.設X是一個代數簇,了是X上的可逆層,若存在一個正整數n,使得牙夕⑧”成為X的甚豐層,則稱丫是...
半豐富層(semiample sheaf)代數簇X上的一類特殊的可逆層.當可逆層丫是半豐富層時,存在m}0使得won,可由整體截面生成.也就是說,牙庵,可以確定一個從X到某個...
甚豐層(very ample sheaf)與一個擬射影簇到射影空間內的嵌人有關的可逆層.設X是一個擬射影簇,丫是X上的可逆層,若存在一個嵌人i;X~屍又,使得}=i"OP...
,所以V上的非常豐富層一一對應於V在射影空間中的表示。假設V是一個維數為d的光滑代數簇,則V上所有的局部d階外微分形式構成一個可逆層 ,叫做V的典範層,它所...
易見主除子對應的可逆層同構於平凡層。兩個除子之和對應的可逆層是原來兩個除子對應之可逆層的張量積。若兩個除子之差為一主除子,則他們定義的線叢是同構的...
皮卡群(Picard group)一種阿貝爾群.指由環空間引出的一種群.環空間(X,OX)的可逆層的同構類所成的群.群的運算由可逆層的張量積所誘導.X的皮卡群記為Pic (X...
典範除子(canonical divisor)是代數簇上的一類特殊的除子。具體地,若X是光滑代數簇,ΩX1是X上的正則1形式芽層,ωX=∧rΩX1,r=dim X,則稱可逆層ωX對應的...
