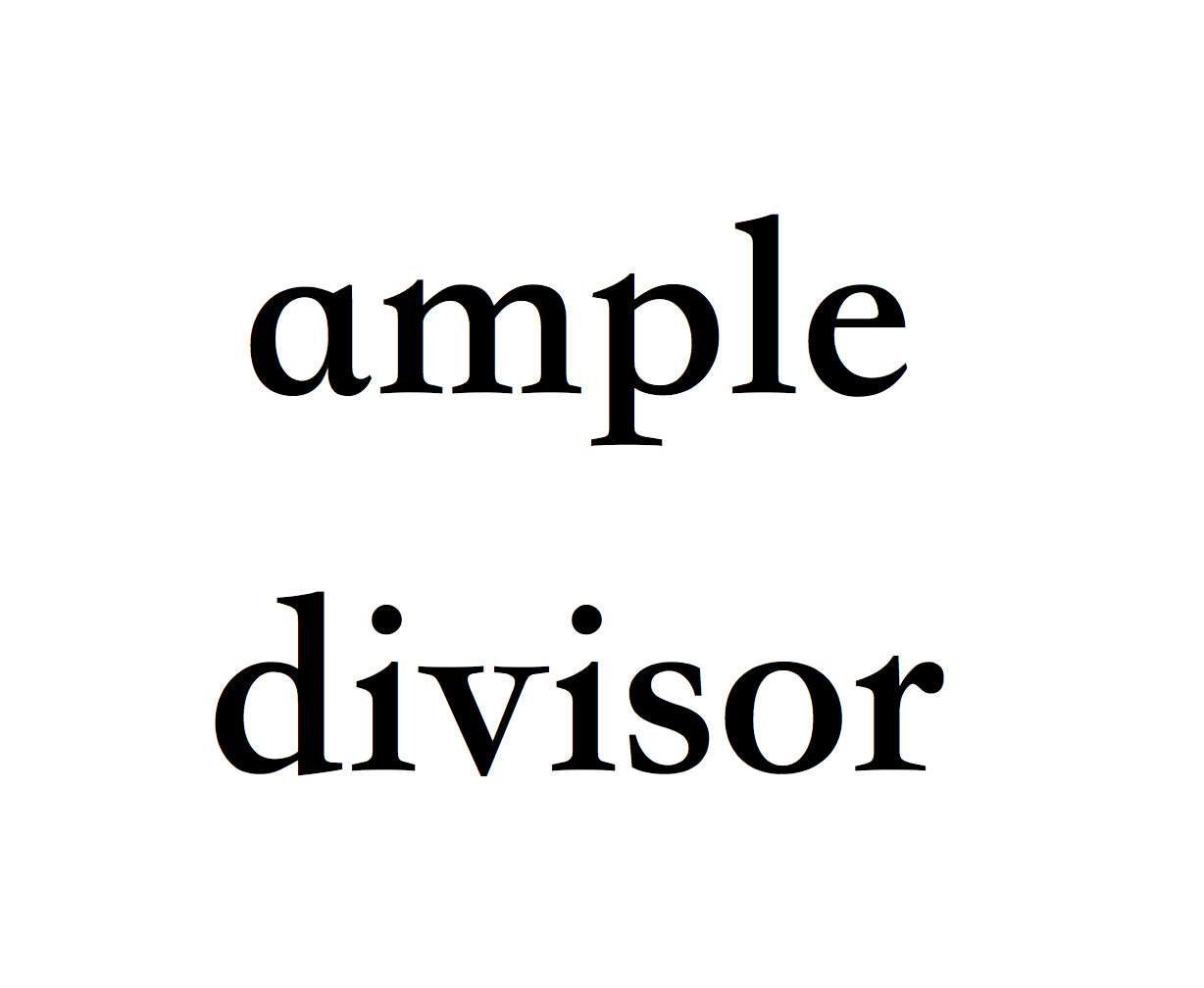豐富除子

豐富除子是代數曲面中最重要的一類除子。 所謂除子， 就是一些不可約的代數曲線的線性組合。豐富除子的乘以充分大倍數後是個非常豐富除子（very ample divisor）。 所謂非常豐富除子， 就是說它是某個超平面截口。 一個射影代數曲面上一定有非常豐富除子。

基本介紹

• 中文名：豐富除子
• 外文名：ample divisor
• 釋義：不可約的代數曲線的線性組合
• 類型：代數曲面中最重要的一類除子
• 概念推廣：射影代數簇

簡介

豐富除子H就是滿足Nakai判別法的除子：HC>0, HH>0, 這裡C是任何不可約曲線， HC是H與C的相交數， HH是H的自交數。

豐富除子的乘以充分大倍數後是個非常豐富除子（very ample divisor）。 所謂非常豐富除子， 就是說它是某個超平面截口。 一個射影代數曲面上一定有非常豐富除子。

射影平面中任何不可約曲線都是豐富除子。

豐富除子的概念也可以推廣到一般的射影代數簇上(就是在射影空間里的代數簇)。

可逆層

設𝒵是概形X上的可逆層，是𝒵的截面，這些截面在任何一點x∈X處的值在𝒪𝗑上生成𝒵𝗑。存在唯一態射使得，這裡是ℙᴺ(k)里的齊次坐標。

如果存在嵌入使得，就稱X上的可逆層𝒵是極豐富的（very ample）。

如果存在正整數n使得𝒵ⁿ是極豐富的，就稱X上的可逆層𝒵為豐富的（ample）。

k上的諾特概形X的可逆層𝒵是豐富的，若且唯若對於X上的每個凝聚層𝒥，存在整數n₀>0使得當n≥n₀時層𝒥⊗𝒵ⁿ由它的整體截面生成。

如果除子D對應X上的一個豐富可逆層𝒵，就稱D為豐富除子。設X是代數閉域k上的真光滑概形，則X上卡吉耶除子D為豐富的若且唯若對每個閉整子概形Y≤X，相交指數取正值，這裡r=dimY。

極豐富和豐富可逆層的概念也可被轉移到解析空間的情形。