代數是數學的一個分支。傳統的代數用有字元 (變數) 的表達式進行算術運算,字元代表未知數或未定數。如果不包括除法 (用整數除除外),則每一個表達式都是一個含有理係數的多項式。代數方法使問題的求解簡化為符號表達式的操作,已滲入數學的各分支。
局部代數(local algebra)是與局部環相應的一類特殊代數。德國數學家菲廷證明了局部代數的重要性質。
基本介紹
- 中文名:局部代數
- 外文名:local algebra
- 領域:代數學
- 對應環:局部環
- 本質:一類特殊代數
- 相關人物:菲廷
概念介紹
代數
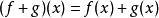
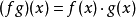
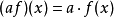
代數是數學的一個分支。傳統的代數用有字元 (變數) 的表達式進行算術運算,字元代表未知數或未定數。如果不包括除法 (用整數除除外),則每一個表達式都是一個含有理係數的多項式。代數方法使問題的求解簡化為符號表達式的操作,已滲入數學的各分支。
局部代數(local algebra)是與局部環相應的一類特殊代數。德國數學家菲廷證明了局部代數的重要性質。
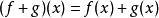
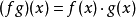
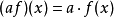
代數是數學的一個分支。傳統的代數用有字元 (變數) 的表達式進行算術運算,字元代表未知數或未定數。如果不包括除法 (用整數除除外),則每一個表達式都是一個...
局部有限代數(locally finite algebra)與局部有限群相平行的概念。若域F上代數A中任意有限個元生成的子代數是有限維的(或冪零的),則稱A是局部有限代數(或局部冪...
《關於代數微局部化的若干問題》是1991年復旦大學授予的一篇論文,作者是沈大慶。...... 《關於代數微局部化的若干問題》是1991年復旦大學授予的一篇論文,作者是沈大慶...
局部化,是分式環的另一名稱,局部化有兩個重要性質,即保持正合性和諾特性質,通過哥爾迪(Goldie,A. W.)等人的工作,局部化方法已套用於非交換環論研究中.例如,...
定義 重複代數(repetitive algebras)由有限維代數構造的一類無限維代數.若n是域k上的有限維代數,D=Homk(一,k)是對偶函子,則Dcn)有自然的n-n雙模結構.n的重複...
局部性質是對局部化保持的性質。由局部性質去掌握整體特性是研究環、模的重要手段。...
代數空間(algebraic space)代數簇和概形概念的推廣。代數空間是阿廷(Artin,E.)引入的,主要目的是為了彌補概形範疇關於許多取商的函子不封閉的缺陷。代數空間關於...
