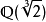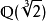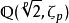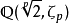基本介紹
- 中文名:正規擴張
- 外文名:Normal expansion
- 領域:數學
- 套用:抽象代數;代數擴張
定義,例子,性質,正規閉包,
定義
正規擴張的定義不止一種,以下三個準則都可以刻畫正規擴張,是三個等價的定義。域擴張L/K是正規擴張若且唯若它滿足以下三個等價條件中任意一個:
- 任意一個K[X]上的不可約多項式,只要它在L中有一個根,那么就可以在L[X]分解成一次因式的乘積(或者說全部的根都在L中)。
例子
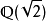
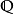
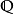

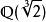
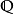
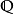
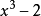
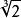

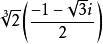


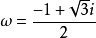
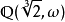

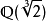

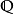
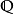

性質
設有域擴張L/K,那么:
1) 如果L是K的正規擴張,並且F是一個子擴張(也就是說有擴張K⊂F⊂L)那么L也是F的正規擴張。
2) 如果L的子域E和F都是K的正規擴張,那么兩者的複合擴張EF(指L的子域中同時包含E和F的最小者)以及兩者的交E∩F也都是K的正規擴張。
正規閉包
設有域擴張L/K,那么總存在域擴張M/L,使得M/K是正規擴張。在同構意義上,最小的這樣的擴張是唯一。即是說,其他的域擴張N/L如果使得N/K是正規擴張,那么總存在N/L的子擴張M'/L,使得M'同構於M。這個唯一的“最小”正規擴張M/L稱為域擴張L/K的正規閉包。
如果L/K是有限擴張,那么它的正規閉包M/L也是有限擴張(因此M/K也是有限擴張)。