分解群是伽羅瓦群的一個子群,它使得這個正規擴張的某個賦值環穩定不變。分解群還是素理想分解因子的固定伽羅瓦子群。
基本介紹
- 中文名:分解群
- 外文名:decomposition group
- 適用範圍:數理科學
定義,定義一,定義二,伽羅瓦群,
定義
定義一
分解群是伽羅瓦群的一個子群,它使得這個正規擴張的某個賦值環穩定不變。
若 N 是域 F 的一個正規擴張,C 是 N 的一個賦值環,在伽羅瓦群 Aut (N/F)中,子集
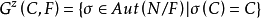
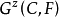
定義二
分解群是素理想分解因子的固定伽羅瓦子群。
若 E/F 為整體域的伽羅瓦擴張,伽羅瓦群為 G,β 為 E 的素理想,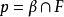 ,則
,則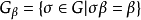 稱為β 的分解群,Gβ 的元素自然地是
稱為β 的分解群,Gβ 的元素自然地是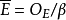 在
在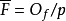 上自同構。若
上自同構。若
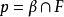
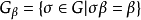
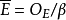
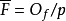
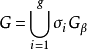
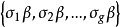
伽羅瓦群
數學中,伽羅瓦群(Groupe de Galois)是與某個類型的域擴張相伴的群。域擴張源於多項式,通過伽羅瓦群研究域擴張以及多項式稱為伽羅瓦理論,以發現者法國天才數學家埃瓦里斯特·伽羅瓦命名。
假設 E 是域 F 的一個擴張(寫成 E/F,讀做 E 在 F 上,英語:E over F)。考慮所有 E/F 的自同構集合(即同構 α 從 E 到自身使得 α(x) = x 對所有 x 屬於 F)。這個自同構集合與函式複合一起組成一個群,有時記做 Aut(E/F)。
如果 E/F 是一個伽羅瓦擴張,則 Aut(E/F) 稱為(擴張)E 在 F 上的伽羅瓦群,通常記做 Gal(E/F)。