輻角原理又稱柯西輻角原理,是複變函數中的一個重要原理,即沿著閉曲線C正向繞行一周后輻角argf(z)的改變數除以2π等於f(z)在C的內部的零點和極點個數的差值。輻角原理可用於求解複變函數的零點或極點個數,也可用於求解方程f(z)=a的根的個數。在自動控制理論中,輻角原理作為奈奎斯特穩定判據的理論基礎,用於判斷單變數系統的穩定性。
基本介紹
- 中文名:輻角原理
- 外文名:Argument Principle
- 別稱:柯西輻角原理
- 所屬學科:複變函數
- 套用1:求解複變函數的零點或極點個數
- 套用2:求解方程f(z)=a的根的個數
- 套用3:奈奎斯特穩定判據的理論基礎
對數留數






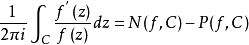



定義



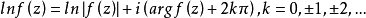

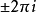
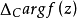
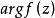
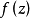
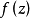

證明

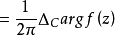
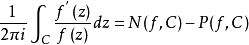

套用


