施圖姆定理

施圖姆定理是一個用於決定多項式的不同實根的個數的方法。這個方法是以雅克·夏爾·弗朗索瓦·施圖姆命名的，但實際上是約瑟夫·傅立葉發現的。施圖姆定理與代數基本定理的一個區別是，代數基本定理是關於多項式的實根或復根的個數，把重根也計算在內，而施圖姆定理則只涉及實根，且不把重根計算在內。

基本介紹

• 中文名：施圖姆定理
• 分類：數學定理、多項式
• 領域：數理科學

施圖姆序列

我們首先從以下不含平方因式的多項式構造一個施圖姆序列：

施圖姆序列是把輾轉相除法套用於X和它的導數X1 = X′時，所得到的中間結果的序列。施圖姆序列由以下公式計算：

也就是說，序列中每一項都是前兩項相除所得的餘數，並將其變號。由於當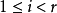 時， ，因此這個序列最終要停止。最後一個多項式，X_r，就是X和它的導數的最大公因式。由於X沒有重根，因此X_r是一個常數。於是，施圖姆序列為：

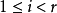
表述

設σ(ξ)為以下序列中符號變化的次數（零不計算在內）：

其中X是不含平方因式的多項式。於是施圖姆定理說明，對於兩個實數a<b，半開區間(a,b]中的不同根的個數為σ(a)−σ(b)。

套用

通過恰當選擇a和b，這個定理可以用來計算多項式的實根的總個數。例如，柯西發現的一個定理說明，係數為ai的多項式的所有實根都在區間[−M,M]內，其中：

除此以外，我們還可以利用下列事實：對於很大的x，以下多項式的符號

是sgn(a_n)，而sgn(P(−x))則是sgn((−1)a_n)。用這種方法，僅僅計算施圖姆序列中首項係數的符號變化，就可以得出多項式的不同實根的個數。通過施圖姆定理的幫助，我們還可以決定某個給定根（例如ξ）是幾重根。確實，假設我們知道ξa和b之間，且σ(a)−σ(b)= 1。那么，ξ是m重根正好當ξ是X_r的m−1重根時（這是因為它是X和它的導數的最大公因式）。

廣義施圖姆序列

設ξ位於緊區間[a,b]內。[a,b]上的廣義施圖姆序列，是實係數多項式(X₀，X₁，……，X_r)的一個有限序列，使得：

1. X(a)X(b) ≠ 0
2. sgn(X_r)在[a,b]內是常數
3. 如果當1 ≤i≤r−1時，X_i(ξ)= 0，那么X_i−1(ξ)X_i+1(ξ)< 0。

我們可以驗證每一個施圖姆序列確實是廣義施圖姆序列。