同底數冪(The same base powers)是指底數相同的冪。同底數冪之間共有5條計算性質,對正指數冪和負指數冪均適用。
基本介紹
- 中文名:同底數冪
- 外文名:The same base powers
- 拼音:tong di shu mi
- 釋義:底數是相同的冪
- 相關計算:同底數冪的乘法,除法等
- 運算性質數目:5條
定義
 同底數冪
同底數冪數冪計算
乘法
除法
 同底數冪的除法
同底數冪的除法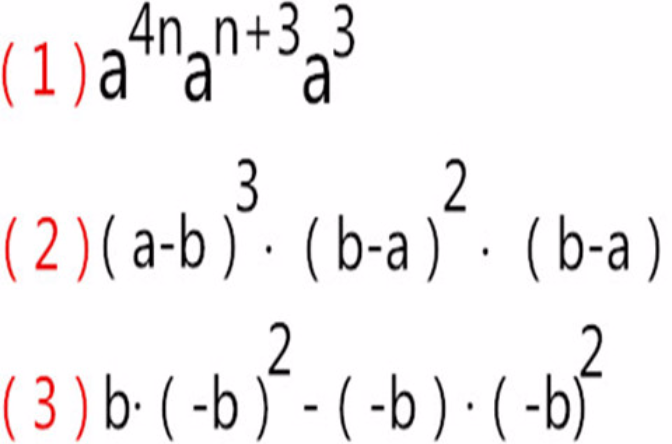
同底數冪(The same base powers)是指底數相同的冪。同底數冪之間共有5條計算性質,對正指數冪和負指數冪均適用。
 同底數冪
同底數冪 同底數冪的除法
同底數冪的除法同底數冪(The same base powers)是指底數相同的冪。同底數冪之間共有5條計算性質,對正指數冪和負指數冪均適用。...
冪運算是一種關於冪的數學運算。同底數冪相乘,底數不變,指數相加。同底數冪相除,底數不變,指數相減。冪的冪,底數不變,指數相乘。
一般地,在數學上我們把n個相同的因數a相乘的積記做a^n。這種求幾個相同因數的積的運算叫做乘方,乘方的結果叫做冪。在a^n中,a叫做底數,n叫做指數。a^n讀作...
同底數冪是指底數相同的冪積的乘方:(axb)^n=a^n×b^n次冪圓冪的定義 編輯 一點P對半徑R的圓O的冪定義如下:OP^2-R^2,所以圓內的點的冪為負數,圓外...
引入負指數冪後,正整數指數冪的運算性質(①~⑤)仍然適用: (a^m)·(a^n)= a^(m+n) ①即 同底數冪相乘,底數不變,指數相加。...
冪是一個漢字,(漢語拼音:mì,注音:ㄇㄧˋ,音同“覓”),意思是指乘方運算的結果。指將自乘次。把冪看作乘方的結果,叫做“n的m次冪”或“n的m次方”。...
單項式相除,把係數、同底數冪分別相除後,作為商的因式;對於只在被除式中含有的字母,則連同它的指數一起作為商的一個因式。注:單項式除以單項式主要是通過轉化為同...
求n個相同因數乘積的運算,叫做乘方,乘方的結果叫做冪(power)。其中,a叫做底數(base number),n叫做指數(exponent)。當aⁿ看作a的n次乘方的結果時,也可讀作“...
22、73也可以看做是乘方運算的結果,這時它們表示數,分別讀作“2的2次冪”、“7的3次冪”,其中2與7叫做底數(base),2與3叫做指數(exponent)。...
指數是冪運算aⁿ(a≠0)中的一個參數,a為底數,n為指數,指數位於底數的右上角,冪運算表示指數個底數相乘。當n是一個正整數,aⁿ表示n個a連乘。當n=0時,...
單項式相除,把係數、同底數冪分別相除作為商的因式,對於只在被除式中出現的字母,則連同它的指數一起作為商的一個因式。說明:兩個單項式相除,只要將係數及同底數...
有理數的指數冪,運算法則要記住。指數加減底不變,同底數冪相乘除。指數相乘底不變,冪的乘方要清楚。積商乘方原指數,換底乘方再乘除。...
單項式除法法則 同底數冪(次方)相除,底數不變,指數相減。參考資料 1. 中國社會科學院語言研究所詞典編輯室.現代漢語詞典(第6版):商務印書館,2012 ...
