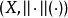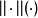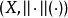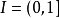模糊賦范空間(fuzzy normed space)是賦范空間的一種推廣,它是一類特殊的模糊拓撲線性空間。模糊賦范空間的概念是吳從炘、方錦暄於1984年給出的,同年,凱茲拉斯(A.K.Katsaras)又給出了另一種定義。
基本介紹
- 中文名:模糊賦范空間
- 外文名:fuzzy normed space
- 所屬學科:數學(模糊數學)
- 簡介:一類特殊的模糊拓撲線性空間
基本介紹,模糊賦范空間的基本性質,
基本介紹
1. ,若且唯若
,若且唯若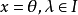 ;
;

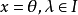
2. ;
;

3.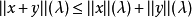 ;
;
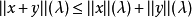
4.若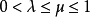 ,則
,則 ,且對任何(x,λ)∈X×I,有0<λn<λ,使得
,且對任何(x,λ)∈X×I,有0<λn<λ,使得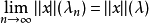 ;則稱
;則稱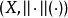 為模糊賦范空間,
為模糊賦范空間,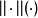 稱為模糊範數。
稱為模糊範數。
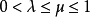

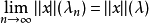
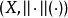
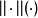
模糊賦范空間的概念是吳從炘、方錦暄於1984年給出的,同年,凱茲拉斯(A.K.Katsaras)又給出了另一種定義。
若X是數域K上的線性空間,則稱X的平衡凸吸收的模糊子集ρ為模糊半范,這裡ρ為平衡的是指,當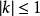 時,kρ⊂ρ,ρ為吸收的是指對任何
時,kρ⊂ρ,ρ為吸收的是指對任何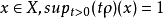 成立。特別地,當
成立。特別地,當
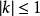
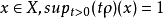

雖然模糊範數的這兩種定義在形式上有很大的差異,但第二種定義的範數與存在映射

1′.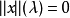 ,若且唯若
,若且唯若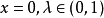 相互惟一確定。
相互惟一確定。
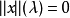
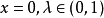
模糊賦范空間的基本性質
下面主要介紹模糊賦范空間中,諸如模糊網收斂、有界模糊集、兩模蝴範數確定同一模糊拓撲以及模糊範數為分明範數的誘出的刻畫等基本性質。
定理1 設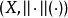 是模糊賦范空間,
是模糊賦范空間,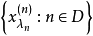 是X中的模糊點網,T是
是X中的模糊點網,T是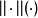 所確定的模糊拓撲,則
所確定的模糊拓撲,則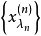 依模糊拓撲T收斂於
依模糊拓撲T收斂於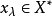 的充要條件為對任給
的充要條件為對任給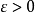 ,存在
,存在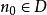 ,使當
,使當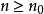 時有
時有
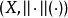
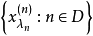
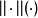
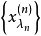
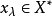
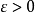
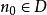
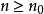
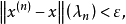
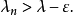
注 顯然定理1對模糊點序列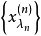 仍然成立,只需將“
仍然成立,只需將“ ”改為“正整數
”改為“正整數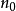 ”。
”。
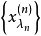

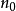
定理2 設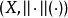 是模糊賦范空間,A是X中模糊集,則A是有界模糊集的充要條件為:
是模糊賦范空間,A是X中模糊集,則A是有界模糊集的充要條件為:
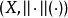
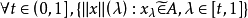
推論1 設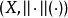 是模糊賦范空間,則
是模糊賦范空間,則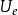 是有界模糊集。
是有界模糊集。
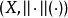
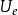
注 對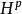 的任何普通子集A,以下兩條件等價:
的任何普通子集A,以下兩條件等價:
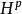
(i) A是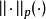 的有界模糊集;
的有界模糊集;
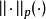
(ii)  對任何
對任何 均為有界集。
均為有界集。


另外,由條件(ii)可以看出: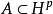 ,關於
,關於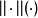 有界,可以理解為在復單位圓盤U內的任何閉子集上
有界,可以理解為在復單位圓盤U內的任何閉子集上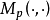 一致有界,這稍弱於按
一致有界,這稍弱於按 範數的有界性。
範數的有界性。
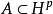
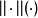
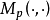

定理3 數域K上的線性空間X的兩模糊範數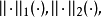 確定同一模糊拓撲T的充要條件為存在
確定同一模糊拓撲T的充要條件為存在
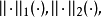
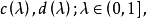
其中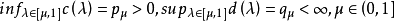 使
使
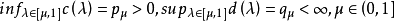
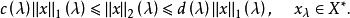
推論2 數域K上的線性空間X的兩等價範數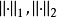 ,所誘出的模糊範數
,所誘出的模糊範數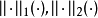 確定同一模糊拓撲。
確定同一模糊拓撲。
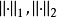
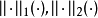
定理4 記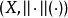 是模糊賦范空間,則
是模糊賦范空間,則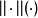 與X上某分明範數
與X上某分明範數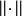 的誘出模糊範數確定同一模糊拓撲的充要條件為:對任何r∈(0,1],
的誘出模糊範數確定同一模糊拓撲的充要條件為:對任何r∈(0,1],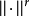 均等價於
均等價於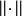 。此處
。此處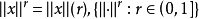 成為X上的一族分明範數。
成為X上的一族分明範數。
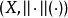
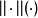
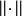
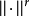
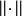
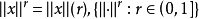
推論3 設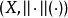 是模糊賦范空間,且對任何r∈(0,1],
是模糊賦范空間,且對任何r∈(0,1], 均為巴拿赫空間,則
均為巴拿赫空間,則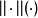 與
與 的誘出模糊範數確定同一模糊拓撲,換句話說
的誘出模糊範數確定同一模糊拓撲,換句話說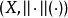 是由巴拿赫空間
是由巴拿赫空間 誘出的。
誘出的。