模糊群

模糊群(fuzzy group)是普通子群的一種推廣，它是群上的一類特殊的模糊子集。設G是群，H是G的模糊子集，滿足：1.對任何x，y∈G， 有H(x，y)≥min(H(x)，H(y));2.H(x)≥H(x^-1);則稱H為G的模糊子群，簡稱模糊群。若H是G的模糊子群，且對任何x，y∈ G，有H(xyx^-1)≥H(y)，則稱H為正規模糊子群。模糊群的概念是1971年由羅森菲爾德(A.Rosenfeld)引入的。

基本介紹

• 中文名：模糊群
• 外文名：fuzzy group
• 所屬學科：數學（模糊數學）
• 簡介：群上的一類特殊的模糊子集
• 提出者：羅森菲爾德(A.Rosenfeld)

基本介紹

模糊代數是專門研究模糊集的各種代數結構的，諸如模糊群、模糊線性空間等，這方面最早的工作見於1971年A.Rosenfeld的文獻，其中首次引入模糊群， 而模糊線性空間則是1977年被引入的。

定義 設G是一個群，A是G的一個模糊子集，稱A是G上的模糊子群(或模糊群)，如果對G中任何x，y滿足：

(1)

(2)

易由以上定義知， ，若e是G的單位元，則對所有 。

從以上關於模糊群的定義看，它是在奠基於精確性經典數學的模糊集合論上，再附加上種種條件而形成的，因而就無一例外地是直接奠基於通常的經典數學之上的了，不過這兒稍有不同的是，模糊群是通常的經典的模糊子集，模糊線性空間是通常的經典線性空間的模糊子集，也就是說，要定義模糊群、模糊線性空間，必須先有通常的群和線性空間，這樣，它們就更在另一層意義上直接依賴於精確性經典數學了。

還有諸多的模糊數學分支，比如模糊測度、模糊數、模糊線性空間、模糊集值映射、模糊賦范空問、模糊拓撲線性空間、模糊拓撲群等等，也都是類似於上面例子，在經典數學理論之下，適當引進模糊子集後加以定義和展開的，因而，就像上面所分析的一樣，也都是直接奠基於精確性經典數學之上的，應該說，模糊數學沿著這個方向發展下去，將是有生命力和卓有成效的，道理也很清楚：我們可以時時藉助於十分成熟的經典數學方法和利用十分豐富的經典數學成果，相信模糊數學的主流，在今後相當長一段時間內仍是這個方向，並且仍可不斷地取得豐碩的結果。

T模糊群

模糊集的模繫結構

模糊集的模繫結構指帶有序結構的一類代數系統，利用它可以統一地描述模糊集的各種運算，設L為具有最小元0和最大元1的格，若映射 滿足以下條件：

1. ;

2.

3.若 ，則有

4.

則稱T為三角模.若三角模T滿足 ，則稱其為T模;若三角模T滿足 ，則稱其為S模.設N為L上的偽補(參見“模糊集”)，如果T模T和S模S滿足 ，則稱T與S為N對偶的，並稱 為模系.對於L模糊集A與B可定義模並、模交與補運算為：

模糊子集的並與交運算是特殊的模並與模交運算。

設F_L(X)為X上所有L模糊集組成的集合，如果 是模系，則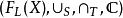 也是模系。

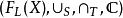
T模糊群的定義

T模糊群是模糊群的一種推廣。設G是群，H是G的模糊子集，T是T模，滿足：

1.對任何 ， 有

2. ；

則稱H為G的T模糊子群，簡稱T模糊群。當T=min時，T模糊群即為模糊群。

T模糊群的概念是1979年由安東尼(J.M.Authony )和舍伍德(J.M.Sherwood)引入的。

模糊群論

模糊群論是研究群的模糊性質的科學。模糊數學與群論的交叉學科。模糊群論的研究對象是各種模糊群的結構、性質及其套用。

1971年勞森弗爾德 (Rosenfold) 首先給出了模糊子廣群、模糊子群的概念，稱之為R-模糊子廣群、R-模糊子群。1979年，安東尼(Anthony) 和瑟烏德 (Shorwood) 利用T-範數重新定義了模糊群，稱之為T-模糊群。1981年戚振開利用模糊點給 出了模糊群的點態化的定義，稱之為點態化模糊群。 作為一門新興的交叉學科，模糊群論有了很大發展。模糊群論的研究內容是十分豐富的，概括起來可分 為：①將分明群中的重要結論推廣到模糊群中；②探 索模糊群相對於分明群所特有的性質；③尋求模糊群的套用。雖然模糊數學的套用觸角已伸向科技領域的許多方面，但模糊群論的套用還有待研究。