高階弗雷歇微分亦稱高階強微分,簡稱高階F微分或高階微分,是 F 微分概念的高階推廣形式。
基本介紹
- 中文名:高階弗雷歇微分
- 外文名:higher Frechet differential
- 適用範圍:數理科學
簡介,一階 F 微分,定義,弗雷歇微分,
簡介
高階弗雷歇微分亦稱高階強微分,簡稱高階F微分或高階微分,是 F 微分概念的高階推廣形式。
一階 F 微分
設 X,Y為賦范線性空間,Ω 是 X 中的開集,f:Ω→Y,x0∈Ω。歸納定義f 在x0的n階F微分,記為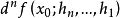 。一階 F 微分
。一階 F 微分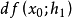 ,即F微分已有定義。
,即F微分已有定義。
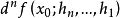
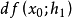
定義
設 f 在x0的某鄰域中有n階F微分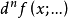 ,若存在有界(n+1)線性運算元
,若存在有界(n+1)線性運算元
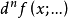
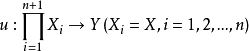
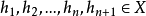
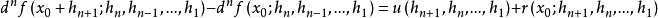
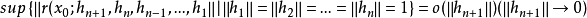

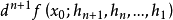
弗雷歇微分
強可微的概念是由弗雷歇於1910年引入的。
設X,Y為賦范線性空間,Ω是X中的開集,f:Ω→Y是映射,x0∈Ω。若存在有界線性運算元A:X→Y ,使得f(x0+h)-f(x0)-Ah=o(||h||),其中o(||h||)/||h||→0(當||h||→0),則稱 f 在x0弗雷歇可微(簡稱F可微)或強可微,A稱為f在x0的弗雷歇導運算元(簡稱F導運算元)或強導運算元,記為df(x0)或f'(x0),Ah稱為f在x0沿h的F微分或強微分,記為df(x0;h)或f'(x0)h。
