基本介紹
定理含義,定理形式,
定理含義
一個信號所含有的能量(功率)恆等於此信號在完備正交函式集中各分量能量(功率)之和。
定理形式
假定A(x)和B(x)都是平方可積的(參照勒貝格測度)複變函數,且定義在R上周期為2π的區間上,分別寫成傅立葉級數的形式:

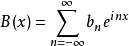
則有:
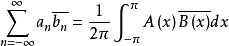


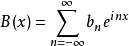
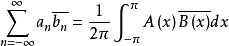
在數學中,帕塞瓦爾定理經常指“傅立葉轉換是么正算符”這一結論;簡而言之,就是說函式平方的和(或積分)等於其傅立葉轉換式平方之和(或者積分)。這個定理產生於...
在數學分析中,以Marc-Antoine Parseval命名的帕塞瓦爾恆等式是一個有關函式的傅立葉級數的可加性的基礎結論。表示可積函式與其傅立葉係數之間關係的恆等式。從幾何...
帕塞瓦爾(Parseval)是一位數學家。提出帕塞瓦爾定理又稱能量守恆定理帕塞瓦爾定理指出,一個信號所含有的能量(功率)恆等於此信號在完備正交函式集中各分量能量(功率)之...
1 簡介 2 定義 3 基本性質 ▪ 線性性質 ▪ 平移性質 ▪ 微分關係 ▪ 卷積特性 ▪ 帕塞瓦爾定理 富里埃變換簡介 編輯 富里埃變換將函式的時域...
3.3.5時域卷積定理3.3.6z域卷積定理(序列相乘)*3.3.7帕塞瓦爾定理3.4Z反變換3.4.1部分分式展開法(partialfractionexpansionmethod)...
附錄C帕塞瓦爾定理附錄D英文縮寫名詞對照表附錄E部分習題答案附錄F部分小測驗答案參考文獻 [3] 參考資料 1. 簡介 .清華大學出版社[引用日期2016-02-03] 2. 通信...
3.6.1 周期信號的功率譜、帕塞瓦爾恆等式3.6.2 非周期信號的能量譜、帕塞瓦爾定理參考資料 1. 信號與線性系統分析基礎 .豆瓣[引用日期2017-10-25] ...
