龐加萊不等式

在數學方面，龐加萊不等式是以法國數學家亨利·龐加萊（Henri Poincaré）命名的Sobolev空間理論的不等式。 不等式允許使用其導數上的邊界及其定義域的幾何來獲取函式上的界限。 這種界限在變化演算的現代直接方法中是非常重要的。 一個非常密切的不等式是弗里德里希不等式。

龐加萊不等式也是拉普拉斯特徵值的一個不等式，即關於最小非零的拉普拉斯特徵值的極大-極小原理，在整體分析和偏微分方程中有重要套用。

基本介紹

• 中文名：龐加萊不等式
• 外文名：Poincare inequality
• 意義：導數泛數值對本身泛數值的關係
• 特徵：拉普拉斯特徵值
• 套用：整體分析和偏微分方程
• 其他不等式：龐加萊-維林格不等式

表示形式

龐加萊不等式(Poincare inequality)是關於函式與其梯度的L^p範數的不等式，龐加萊不等式主要描述的是函式的廣義導數的泛數值對該函式本身的泛數值的限制關係。

龐加萊不等式也是拉普拉斯特徵值的一個不等式，即關於最小非零的拉普拉斯特徵值的極大-極小原理，在整體分析和偏微分方程中有重要套用。

設含於一個寬度為h的條形區域內，， 則下列龐加萊不等式成立：

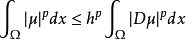
而不等式：

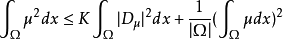
亦稱為龐加萊不等式。若集合N={x∈Ω|u(x)=0}的中的測度|N|>0，則：

龐加萊 - 維林格不等式

設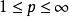，Ω是具有Lipschitz邊界的n維歐幾里德空間Rn的有界連線的開放子集（即Ω是Lipschitz域）。 那么存在一個常數C，其值只取決於Ω和p，使得對於Sobolev空間W1，p（Ω）中的每個函式u，都有：

其中：是在上的平均值，表示區域上的勒貝格測度。當是球區域時，上述不等式叫做a(p,p)-龐加萊不等式。對更為普通的區域，上述不等式更為人熟知的名字是索伯列夫不等式。

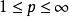
龐加萊常數

龐加萊不等式中的最優常數C有時被稱為域Ω的龐加萊常數。一般來說，確定龐加萊常數是一個非常艱巨的任務，取決於p的值和域Ω的幾何形狀。但是，某些特殊情況是易處理的。例如，如果Ω是具有直徑d的有界，凸的Lipschitz域，則對於p = 1，龐加萊常數最多為d / 2，d / π（Acosta&Durán2004； Payne&Weinberger 1960），這是對龐加萊常數在單直徑方面的最佳估計。對平滑的函式來說，這可以被理解為對函式的級集合的等效不等式的套用。 在一個維度上，這是Wirtinger對函式的不等式。

然而，在某些特殊情況下，可以具體確定常數C。例如，對於p = 2，眾所周知，在單位等腰直角三角形的域上，C = 1 /π（<d /π其中d = 根號2）。

此外，對於平滑有界的域Ω，由於在空間W_ {0} ^ {1,2}（Ω）中的拉普拉斯運算元的瑞利商通過與（負）拉普拉斯運算元的最小特徵值λ1相對應的特徵函式來最小化Ω，這是一個簡單的結果，對任意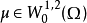，都有：

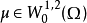
此外，常數λ1是最優的。