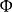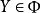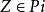基本介紹
定義,緊支撐,奇支集,支撐族,
定義
特別地,在機率論中,一個機率分布的支撐集是隨機變數的所有可能值組成的集合的閉包。
緊支撐
一個函式被稱為是緊支撐於空間X的,如果這個函式的支撐集是X中的一個緊集。例如,若 X是實數軸,那么所有在無窮遠處消失的函式都是緊支撐的。事實上,這是函式必須在有界集外為0的一個特例。在好的情形下,緊支撐的函式所構成的集合,在所有在無窮遠處消失的函式構成的集合中,是稠密集的,當然在給定的具體問題中,這一點可能需要相當的工作才能驗證。例如對於任何給定的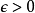 ,一個定義在實數軸X上的函式 f在無窮遠處消失,可以粗略通過選取一個緊子集 C來描述:
,一個定義在實數軸X上的函式 f在無窮遠處消失,可以粗略通過選取一個緊子集 C來描述:
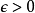
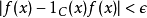
其中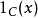 表示 C的指示函式。
表示 C的指示函式。
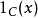
注意,任何定義在緊空間上的函式都是緊支撐的。
當然也可以更一般地,將支撐集的概念推廣到分布,比如狄拉克函式:定義在直線上的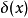 。此時,我們考慮一個測試函式F,並且 F是光滑的,其支撐集不包括 0。由於
。此時,我們考慮一個測試函式F,並且 F是光滑的,其支撐集不包括 0。由於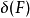 (即
(即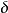 作用於F)為 0,所以我們說
作用於F)為 0,所以我們說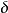 的支撐集為
的支撐集為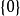 。注意實數軸上的測度(包括機率測度)都是分布的特殊情況,所以我們也可以定義一個測度支撐集。
。注意實數軸上的測度(包括機率測度)都是分布的特殊情況,所以我們也可以定義一個測度支撐集。
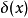
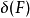
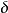
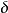
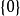
奇支集
在傅立葉分析的研究中,一個分布的奇支集或奇異支集有非常重要的意義。 直觀地說,這個集合的元素都是所謂的奇異點,即使得這個分布不能局部地看作一個函式的點。
例如,單位階躍函式的傅立葉變換,在忽略常數因子的情況下,可以被認為是1/x,但這在x=0時是不成立的。所以很明顯地,x=0是一個特殊的點,更準確地說,這個分布的傅立葉變換的奇支集是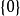 ,即對於一個支撐集包括0的測試函式而言,這個分布的作用效果不能表示為某個函式的作用。當然這個分布可以表示為一個柯西主值意義下的瑕積分。
,即對於一個支撐集包括0的測試函式而言,這個分布的作用效果不能表示為某個函式的作用。當然這個分布可以表示為一個柯西主值意義下的瑕積分。
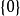
對於多變數的分布,奇支集也可以更精確地被描述為波前集,從而可以利用數學分析來理解惠更斯原理。奇支集也可以用來研究分布理論中的特殊現象,如在試圖將分布'相乘'時候導致的問題(狄拉克函式的平方是不存在的,因為兩個相乘的分布的奇支集必須不相交)。