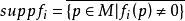單位分解存在性定理

單位分解存在性定理（theorem of existence ofpartition of unity）是在某些條件下單位分解的存在定理。

基本介紹

• 中文名：單位分解存在性定理
• 外文名：theorem of existence ofpartition of unity
• 適用範圍：數理科學

簡介

單位分解存在性定理是在某些條件下單位分解的存在定理。

該定理斷言：若M是微分流形，{U_α|α∈A}是M的任一開覆蓋，則存在從屬於該覆蓋的可數的單位分解{𝜙_i}，對於每個i，supp 𝜙_i是緊集。或去掉緊支集條件，存在從屬於覆蓋{U_α|α∈A}的單位分解{𝜙_α}（即supp 𝜙a⊂U_α），且至多有可數個𝜙_α不恆為零。

套用

微分流形的仿緊性保證了它具有單位分解的性質。

這個性質能把局部函式擴並為整體函式，反過來也能把整體函式分解為局部函式來研究。

單位分解

在微分幾何學中，單位分解是一種特殊的開覆蓋，指微分流形上的一種開覆蓋。

C^k流形M上的C^k單位分解是M上一族C^k函式{f_i|i∈Z}，它具有以下性質：

1、對M的每一點p，f_i(p)≥0且。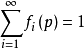

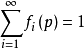
2、函式f_i的支集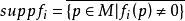組成的集族{suppf_i}是M的局部有限的覆蓋，C^k流形M為仿緊時，對於M的任一開覆蓋{U_α}，必存在從屬於{U_α}的C^k單位分解{f_i}，即{f_i}還有下述性質：對每個i，f_i的支集suppf_i是緊緻的，並且有開集U_α使得suppf_i⊂U_α。