泛函分析中研究運算元的譜的理論。運算元的譜的概念是有限維矩陣的特徵值概念的推廣。力學、物理和工程技術中的大量問題在一定的條件下可以歸結為數學上代數方程、微分方程、積分方程或微分積分方程等的求解問題。在對這些方程求解問題的研究獲得豐富成果的基礎上,逐漸形成了一般的運算元的譜的理論(這裡主要指線性運算元)。
基本介紹
- 中文名:譜論
- 外文名:spectral theory
- 適用範圍:數理科學
簡介,套用,相關概念,譜運算元,譜測度,譜半徑,
簡介
譜論通過分析線性運算元譜的性質來研究該運算元的結構。例如,用簡單運算元重新構造該運算元、研究運算元不變子空間的性質、運算元在一定範圍的函式演算等。
套用
譜論是泛函分析的一個極為重要分支。對於有限維空間上的運算元,其譜論就是研究對應矩陣的本徵值、本徵空間以及若爾當分解等性質。無限維空間上緊線性運算元的譜理論有些類似於有限維情況。例如,緊運算元的譜集是至多可數的且 0 是唯一可能的聚點。
希爾伯特空間上的正規運算元都有譜分解。微分運算元的譜理論是譜理論的重要方面,在微分方程、量子力學等理論中有著廣泛的套用。
相關概念
譜運算元
巴拿赫空間上具有某種譜分解性質的一類運算元,它是若爾當型矩陣在無窮維空間的一種推廣。 自共軛的常微分方程的邊值問題的研究發展成希爾伯特空間上自伴運算元(或自共軛運算元)的譜論,這是20世紀數學上的重大成就。
譜運算元是由鄧福德(N.Dunford)於 20 世紀 50年代引入的,是矩陣若爾當型在無限維的推廣。
設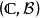 為複平面的博雷爾可測空間,
為複平面的博雷爾可測空間, 是巴拿赫空間,
是巴拿赫空間, 。如果存在
。如果存在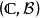 到
到 的譜測度
的譜測度 滿足:
滿足:
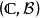


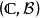


①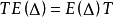 ;
;
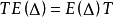
② ;
;

③ 在
在 上是一致有界的,即存在
上是一致有界的,即存在 ,使得
,使得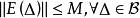 ,則稱 T 為譜運算元,稱
,則稱 T 為譜運算元,稱 為 T 的譜分解。
為 T 的譜分解。



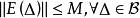

譜運算元的譜分解是唯一的。若譜測度 E 具有緊支集 ,則稱運算元
,則稱運算元 為純量運算元 (scalar operator)。T 是譜運算元,N 是廣義冪零運算元且
為純量運算元 (scalar operator)。T 是譜運算元,N 是廣義冪零運算元且 。
。



類似地,將條件①變為 ,則可以定義無界的譜運算元。
,則可以定義無界的譜運算元。

此時,一般不再有分解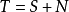 。
。
譜測度
設B為複平面C上波萊爾子集構成的σ代數。
若E是從B到巴拿赫空間X上射影運算元族之同態映射,並且E(·)還是一致有界的,即E(C)=I,E(C\σ)=I-E(σ),
‖E(σ)‖≤K(常數) (σ∈B),則稱{E(σ)|σ∈B}為譜測度。這裡運算元A∨B=A+B-AB。
譜半徑




