向量函式(vector function)是向量分析中的基本概念。給出一個點集CU,並在G上選定一個坐標系.若對於G中每一個點p,總有三維歐氏空間R3中的一個確定的向量r和它對應,則稱r為定義在CU上的一個向量函式。
基本介紹
- 中文名:向量函式
- 外文名:vector function
- 適用範圍:數理科學
雅可比矩陣


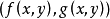
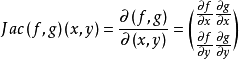



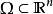

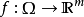

套用
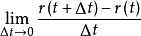

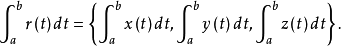

向量函式(vector function)是向量分析中的基本概念。給出一個點集CU,並在G上選定一個坐標系.若對於G中每一個點p,總有三維歐氏空間R3中的一個確定的向量r和它對應,則稱r為定義在CU上的一個向量函式。


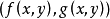
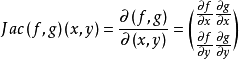



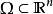

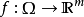

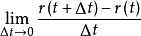

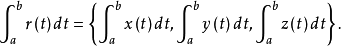
向量函式(vector function)是向量分析中的基本概念。給出一個點集CU,並在G上選定一個坐標系.若對於G中每一個點p,總有三維歐氏空間R3中的一個確定的向量r和它...
我們知道,一元函式是一個由定義域到值域的映射,其定義域與值域都是一維數集.我們要研究的向量值函式是指分量都是關於同一自變數的一元函式,就是說 n 元向量值...
向量空間又稱線性空間,是線性代數的中心內容和基本概念之一。在解析幾何里引入向量概念後,使許多問題的處理變得更為簡潔和清晰,在此基礎上的進一步抽象化,形成了與...
隨機向量分布函式(distribution function ofrandom vector)能完全描述隨機向量機率分布的多元函式。...
概周期向量函式(almost periodic vector func-dons)一類特殊的向量函式.如果向量值函式f(t>_ (.fi (t) ,.fz (t) , ... ,.fn (t) )T的每一元素.f=...
向量線(vector line)是向量場中具有特定意義的曲線,指其切線方向與場中向量一致的向量場中的曲線。設f是定義在區域Ω⊆R3上的向量場,Γ是Ω中的光滑曲線,若...
強可測向量值函式(strongly measurable vec-for valued function)可測數值函式概念在賦范線性空間上的推廣.設(月,了,產)是測度空間,二((t)是定義在月上而且...
弱可測向量值函式(weakly measurable vectorvalued function)是可測數值函式概念在賦范線性空間上另一種重要的推廣。...
向量值積分,普通(數值的)積分在向量值上的推廣。在分析數學的各分支中,因不同的要求,需要種種或是向量值函式的積分或是關於向量值測度的積分。向量值函式的積分...
在這篇文章內,向量與其量值分別用粗體與斜體表示,這條目陳列一些常用的向量恆等式。...
向量球諧函式(Vector spherical harmonics)是套用於球坐標系的拉普拉斯方程式的向量解,是球諧函式的向量衍伸形式。在必須計算向量場的電動力學等領域中被廣泛套用。....
向量邏輯是一種建基於矩陣代數的邏輯模型。它假設邏輯真值可成為一種向量,而一元和二元謂詞演算皆以矩陣的算法進行。...
在數學裡,線性函式是指那些線性的函式,但也常用作一次函式的別稱,儘管一次函式不一定是線性的(那些不經過原點的)。線型函式是一個比較恰當的同義詞。...
初始向量(IV, initialization vector或SV, starting variable)或稱初向量,是一個固定長度的輸入值。...
設H為線性空間,[·,·]是H上的一個雙線性埃爾米特泛函,x∈H,當x分別滿足[x,x]>0時,稱x為正性向量。...
ROT: Rate of turning 旋迴轉速,又稱 轉向率。在物理中等於▽×符號,求向量旋度。ROT:reconstitution-operation-transfer,重構-運營-移交。PPP模式的一種。下屬模式...
形如f(x)=an·x^n+an-1·x^(n-1)+…+a2·x^2+a1·x+a0的函式,叫做多項式函式,它是由常數與自變數x經過有限次乘法與加法運算得到的。顯然,當n=1時...
其中U、V表示一組向量,U是向量的橫坐標(x分量),V是向量的縱坐標(y分量)。該調用格式將在水平軸上等間隔的把這些向量用帶箭頭的線繪製出來。具體算法可通過...
設H為線性空間,[·,·]是H上的一個雙線性埃爾米特泛函,x∈H,當x滿足[x,x]=0時,稱x為零性(或迷向)向量。...
目標函式f(x)就是用設計變數來表示的所追求的目標形式,所以目標函式就是設計變數的函式,是一個標量。從工程意義講,目標函式是系統的性能標準,比如,一個結構的最...
向量場是由一個向量對應另一個向量的函式。向量場廣泛套用於物理學,尤其是電磁場。...... 向量場是由一個向量對應另一個向量的函式。向量場廣泛套用於物理學,尤...
權向量又稱為權重向量。權向量ωm中的權係數ωi的大小代表相應目標fi在多目標最最佳化問題中的重要程度,ωi越大表示fi在問題中越重要,反之,越小的ωi表示fi越不...
在初級代數與解析幾何,線性函式是只擁有一個變數的一階多項式函式。因為,採用直角坐標系,這些函式的圖形是直線,所以,這些函式是線性的。線型函式是一個比較恰當的...
cumsum是matlab中一個函式,通常用於計算一個數組各行的累加值,函式用法是B = cumsum(A,dim),或B = cumsum(A)。...
