基本介紹
- 中文名:托姆定理
- 外文名:Thom theorem
- 適用範圍:數理科學
簡介,推廣,托姆空間,
簡介
該定理斷言:設k>n+1,萬有托姆空間的同倫群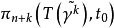 標準同構於定向配邊群Ωn。
標準同構於定向配邊群Ωn。
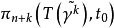
類似地,與未定向萬有叢相聯繫的同倫群 標準同構於未定向配邊群Nn。
標準同構於未定向配邊群Nn。

推廣
由托姆定理得出關於配邊群的托姆定理:若n≢0(mod4),則定向配邊群Ωn是有限的,若n=4r,則Ωn是一個有限生成群,其秩為r的劃分數p(r)。
托姆空間
托姆空間是某種特殊的商空間。
設子是k平面叢(具有歐氏度量),A⊂E(ξ)是全空間中滿足|v|≥1的全體向量v所組成的子集,則當E(ξ)中的A縮為一點,所對應的商空間E(ξ)/A稱為ξ的托姆空間,記為T(ξ)。A縮成的點記為t0,則其補T(ξ)\{t0}由滿足|v|<1的向量v∈E(ξ)組成。
