基本介紹
解釋
例子
性質
導群

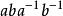
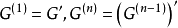



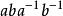
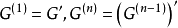

可解群的概念產生於描述其根可以只用根式(平方根、立方根等等及其和與積)表示的多項式所對應的自同構群所擁有的性質。在數學的歷史中,群論原本起源於對五次方程及...
群是一種只有一個運算的、比較簡單的代數結構;是可用來建立許多其他代數系統的一種基本結構。可解群是一種重要的群類。即可由交換群經有限步疊加而得的群。局部...
廣義可解群(generalized soluble group)無限群論的重要研究對象之一,泛指滿足某些群論性質的群,這些群論性質在有限群中等價於群的可解性.由於在一般的廣義可解群中...
有限群是具有有限多個元素的群。群論的重要內容之一。其所含元素的個數,稱為有限群的階。有限群可分為兩大類:可解群與非可解群(特別包括非交換單群)(見群...
可解的有限呈示群是目前無限群研究的重要對象。 [2] 有限生成群群 編輯 群是一種只有一個運算的、比較簡單的代數結構;是可用來建立許多其他代數系統的一種基本...
其所含元素的個數,稱為有限群的階。歷史上,抽象群論的許多概念起源於有限群論。有限群可分為兩大類:可解群與非可解群(即單群)。 半單群(semisimple group)...
有限群可分為兩大類:可解群與非可解群(即單群)。有限群的研究起源很早,其形成時期是與柯西、拉格朗日、高斯、阿貝爾以及後來的伽羅瓦、若爾當等人的名字相聯繫的...
1.無限的可解SD2-群,數學學報,35:3(1992),339-349.2.有限商群的真正規子群是2-生成的多重循環群,數學年刊,15A:3(1994), 255-261....
由此,《從一元一次方程到伽羅瓦理論》在討論了集合論後,用近代方法詳細闡明了對稱群、可遷群、可解群、有限擴域、代數擴域、正規擴域以及伽羅瓦理論等,同時又...
這樣決定的群系F稱為由{F(p)}局部定義的群系,簡稱F為局部系;{F(p)}稱為F的定義系。從群對它的各個主因子的作用情況來研究群,是有限可解群論的常用研究...
具有有限多個元素的群,是群論的重要內容之一。其所含元素的個數,稱為有限群的階。歷史上,抽象群論的許多概念起源於有限群論。有限群可分為兩大類:可解群與非...
亞阿貝爾群(metAbelian group)是一種可解群。指導出列長度至多為2的群。設G是群,若G有導出列 ,則稱G為亞阿貝爾群。設G是群,若G有循環的正規子群N,使得G...
1770年,拉格朗日在討論代數方程根之間的置換時,首先引入群的概念,而它的名稱,是伽羅華在1830年首先提出的。 [1] 博雷爾子群(Borel subgroup)是代數群的一類可解...
根群((radical grow p)一種由升列定義的廣義可解群.若群G具有因子為冪零群的一個升列,則稱G為根群.根群類是很有用的廣義可解群類,因為它包含所有的可...
SN群((SN-group)常見的由廣義序列定義的廣義可解群之一若群具有一個因子為阿貝爾群的列,則稱G為SN群.特別地,若群G具有一個因子為阿貝爾群的正規列,則稱G為...
剩餘交換群(residually commutable group )一種特殊的廣義可解群.若對群的任意兩個非平凡元素a和b,且a和b中至少有一個元素不屬於}a,b}0,其中「a,b}`‘...
