基本介紹
- 中文名:冪零群
- 外文名:Nilpotent group
- 學科:數學
- 屬性:阿貝爾群
- 提出者:謝爾蓋切爾尼科夫
- 類似術語:李群
簡介
定義

舉例
術語解釋

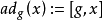
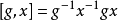
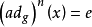

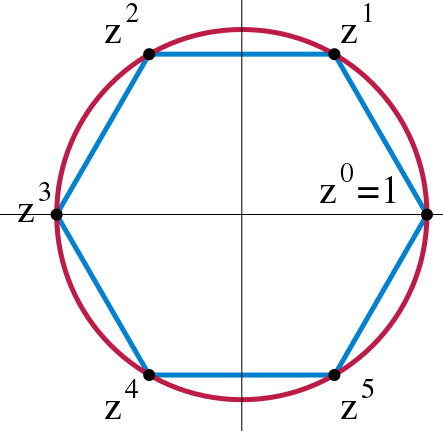


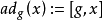
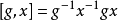
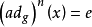

在群體理論中,冪零群是“差不多的阿貝爾”群體。 這個想法的出現是由於冪零群是可解的,而對於有限的冪零群來說,是可以超解的(supersolvable)。 這個概念被...
廣義冪零群(generalized nilpotent group)無限群論研究的重要對象之一泛指滿足某些群論性質的群,這些群論性質在有限群中等價於群的冪零性.由於在有限群中冪零性有...
有限群論無論是從理論本身還是從實際套用來說,都占有突出地位,它中的置換群、可解和非可解群、冪零群、以及群表示論等等,都是重要的研究對象,總之,其內容十分...
z群(Z-group)一種由群的廣義序列定義的非局部冪零的廣義冪零群.它本身又包含若干種特殊類型.若群G有一個中心列{no,vo I aE }'},即對萬中的所有序數。,...
18.關於多重循環群的兩個結果,數學年刊,21A∶6(2000),745-748.19.有限秩的可解群的一個冪零條件,數學年刊,22A∶3(2001),365-368....
在數學中,特別是在群體理論和李群的領域中,中心列是一種普通的子群或李代數,表達了幾乎無關緊要的概念。但對於群體來說,,這個群是一個冪零群,對於矩陣環,這...
p群(p-group)一種特殊的有限群.指每元之階均為p之冪的群,這裡p表示一個固定素數...... 對整個群的性質有重大影響.有限冪零群的研究可歸結為有限p群的研究...
1.5 p-群和冪零群………26 1.5.1 冪零群………26 1.5.2 冪零正規子群………29 1.6 群的正規和次正規結構………32 1.6.1 可解群………32 1.6.2 π...
剩餘中心群(residually central group)構成一個比Z群範圍更大的廣義冪零群類。...... 中心群(residually central group)[1] 構成一個比Z群範圍更大的廣義冪零群...
李正興,海進科,有限冪零群通過對稱群擴張的整群環的正規化子性質,數學學報海進科,戈升波,有限群整群環的正規化子性質,中國科學,45(6)(2015) [2] ...
菲廷(德語:Fitting)定理是群論中冪零子群的一條定理,由漢斯·菲廷證明。定理敘述如下:若M和N是群G的冪零正規子群,則其乘積MN也是G的冪零正規子群。若M是冪...
關於弗羅貝尼烏斯群有一個著名猜想:弗羅貝尼烏斯核是冪零群。這個猜想於20世紀60年代初被湯普森(Thompson,J.G.)證實。[2] 一個抽象群G,若它有一個子群H,...
[6] 郭秀雲,岑嘉評,有限群的極小子群與 P 冪零性,中國科學,32(2002)782--790。[7] Guo Xiuyun and Shum K.P., The influence of minimal subgroups ...
它套用於證明以下陳述:所有有限冪零群都是的西羅子群的直積。若P是西羅子群、G是有限群, 。更一般的結果:若P是西羅子群、G是有限群,且 ,則 。 [1] ...
貝爾群(Baer group)以有限生成子群的次正規性為特徵的特殊類型的廣義冪零群.設H和K是群G的有限生成的冪零子群,記J= (H,K>.若H和K在G內是次正規的,則...
§2.9 冪零群與超可解群§2.10 群的構造§2.11 交換群的結構§2.12 群對稱性的套用第3章 群表示論§3.1 結合代數§3.2 有限維代數§3.3 半單代數...
算術群是較為廣泛的一種群,諸如有限群、有限生成的交換群、無撓的有限生成冪零群以及有限生成的非交換自由群等都是算術群。...
§12 可解群和冪零群第2章 環論§1 基本概念§2 環的同構定理§3 同態的套用§4 各類整環§5 多項式環第3章 域論§1 域的擴張...
1. 鐘祥貴,李世榮.冪零群中非正規循環子群的共軛類數,數學研究與評論, 2006(26)3。2. 鐘祥貴。二次極大子群中2階及4階循環子群擬中心的有限群,數學雜誌,...
5.4無限冪零群和可解群6李群6.1李群的發展歷史6.2李變換群6.3基靈和嘉當的工作6.4李代數理論6.5整體李群7代數群第三篇拓撲學...
在內容上去掉了“冪零群與可解群”和“n(≥5)次一般方程的根式不可解性”兩節,把它們改成兩個附錄.我們也將正文中可略講或只做簡介的內容改用楷體字印刷....
4.3 Sylow子群 4.4 有限單群 4.5 群的直積 4.6 可解群與冪零群 4.7 Jordan-Holder定理 4.8 自由么半群與自由群 4.9 點群 第5章 模 5.1 自...
弱s* -擬正規嵌入子群、次正規嵌入子群等概念,並利用這些特殊子群研究有限群的結構,給出了有限可解群、超可解群及冪零群的性質和結構的一系列刻畫,得到了...
