G群的上中心列(或上升中心列)是一個子群列。
在數學中,特別是在群體理論和李群的領域中,中心列是一種普通的子群或李代數,表達了幾乎無關緊要的概念。但對於群體來說,,這個群是一個冪零群,對於矩陣環,這是一個顯式表達式,在某些基礎上,矩陣環完全由上三角矩陣和常數對角線組成。
基本介紹
- 中文名:上中心列
- 外文名:Upper central series
- 領域:群理論
- 屬性:子群、李群
- 性質:冪零群
- 相關名詞:下中心列
簡介,上下中央列的聯繫,中心列,
簡介
G群的上中心列(或上升中心列)是一個子群列。

每一個繼承群都有這樣的定義:
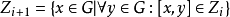
並且被稱為G的第i箇中心(第二中心、第三中心等)。
在這種情況下,Z1是G的中心,對於每一個繼承群,因子群Zi+1/Zi是G/Zi的中心,被稱為上中心列商。
對於無限群,一個群可以通過遞歸繼續成為上中心列:極限序數是λ,定義
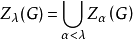
這個過程的極限(高中心的結合)被稱為群的超中心。
如果在整個群體中,超限的上中心列穩定下來,那么這個群稱為超中心。超中心群具有許多冪等群的性質,例如正常的條件(適當子群的正態化)、coprime秩序交換的元素,以及周期性的超中央組是它們的Sylow p -子群的直接和(Schenkman 1975,Ch . 3)。對於每一個序數λ有G組Zλ(G)= G,但Zα(G)≠Gα<λ,(Gluškov 1952)和(1956年McLain)。
上下中央列的聯繫
下中心列和上中心列之間有各種各樣的聯繫(Ellis 2001),特別是對冪零群。
最簡單的是,如果只有當LCS在第一步中終止時(轉換子子群是不太重要的),並且只有當UCS在第一步穩定時(該中心是整個群),那么這個群就是阿貝爾群。更一般地,對於一個冪零群,LCS的長度和UCS的長度(被稱為群的冪零級)。
然而,若且唯若LCS是完美的時候,它在開始就會很穩定,而UCS若且唯若它沒有中心的時候穩定在第零步,這是不同的概念,表明LCS的長度和UCS(解釋為穩定之前)長度一般不需要一致。
一個叫做Grun的引理陳述,對於一個完美的群體,UCS總是第一步就穩定了。然而,一個沒有中心的群可能有一個很長的低的中心列。
中心列
在數學中,特別是在群體理論和李群的領域中,中心列是一種普通的子群或李代數,表達了幾乎無關緊要的概念。但對於群體來說,,這個群是一個冪零群,對於矩陣環,這是一個顯式表達式,在某些基礎上,矩陣環完全由上三角矩陣和常數對角線組成。
這裡使用群體理論的語言;類似的項用於李代數。
下中心列和上中心列(也被稱為下降中心列和提升中心列)是特徵系列,儘管有名字,但它們只有在一個群體是冪零的情況下是中心列。
