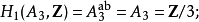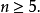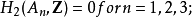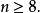基本介紹
基本性質,共軛類,例子,自同構群,特殊同構,子群,群同調,阿貝爾化,舒爾乘子,
基本性質
群 An 是阿貝爾群,若且唯若 n ≤ 3,單若且唯若 n = 3 或 n ≥ 5。注意 A3 事實上是 3 階單群。A1 與 A2 是 1 階群,一般不稱為單的,而 A4 有一個非平凡正規子群從而不單。A5 是最小非阿貝爾單群,階數為 60,也是最小不可解群。
共軛類
在對稱群中,An的共軛類由有相同輪換型的元素組成。但是如果輪換類型只由沒有兩個長度相等的奇數長的輪換組成,這裡長為 1 的輪換包含在輪換型中,則對這樣的輪換型恰有兩個共軛類 (Scott 1987,§11.1, p299)。
例如:
- 兩個置換(123) 與 (132) 有相同的輪換型從而在 S3中共軛,但在 A3中不共軛。
- 置換 (123)(45678) 與其逆 (132)(48765) 有相同的輪換型所以在 S8中共軛,但在 A8中不共軛。
例子
4 階交錯群是 A4= {e, (123), (132), (124), (142), (134), (143), (234), (243), (12)(34), (13)(24), (14)(23)} 。
自同構群
對稱群和交錯群的自同構
對n> 3,除了n= 6,An的自同構群就是 Sn的自同構群,其內自同構群為An外自同構群為Z2;外自同構來自用一個奇置換共軛。
對n= 1 與 2,自同構群平凡。對n= 3 自同構群是Z2,其內自同構群平凡外自同構群為Z2。
A6的外自同構群是克萊因四元群V=Z2×Z2,這也是S6的自同構群。A6另外的自同構將三輪換(比如 (123))與 3型元素(比如 (123)(456))交換。
特殊同構
在小交錯群與小李型群之間有一些同構。他們是
- A4同構於 PSL2(3) 以及手征性四面體對稱之對稱群。
- A5同構於 PSL2(4),PSL2(5),以及手征性二十面體對稱之對稱群。
- A6同構於 PSL2(9) 與 PSp4(2)'。
- A8同構於 PSL4(2)。
更顯然有 A3同構於循環群Z3,以及 A1與 A2同構於平凡群(也是 SL1(q)=PSL1(q) 對任何q)。
子群
A4是說明拉格朗日定理的逆命題一般不成立的最小群:給定一個有限群G和 |G| 的一個因子d,不一定存在G的一個d階子群。群G=A4,階為 12,沒有 6 階子群。有三個元素的子群(由三個對象的輪換旋轉生成)再加上任何一個其它元素生成整個群。