舒爾乘子(Schur multiplier)一類特殊的映射,是群的二次同調群.設G為有限群,A為任一阿貝爾群,用符號Cz (G; A)表示GXG到A中的所有映射之集,在Cz (G; A)中定義加法如下:對任意的(二,y> EGXG,f,hEC2(G;A>,規定(.f+h) (x, y)=f(x,y)+h(x,y),在此加法下CZ (G ; A)成為一個交換群.設BZ(G;A)是由形為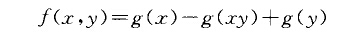
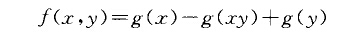
的.fECZ(G;A)所生成的子群,其中g為G到A的某一映射.再設Z2 (G; A)是對任意二,y,zEG滿足:

的.fEC2(G;A)所生成的子群,從而,BZ<G;A)}ZZ (G; A).設HZ (G;A) -Z} (G; A)/BZ (G; A),稱H2 CG; A)為係數在A中的G的二次同調群.群HZ(G;K*)稱為G的舒爾乘子,其中K‘是特徵為零的代數閉域中非零元素所成的乘法群.當G為單群時,舒爾((Schur,I.)證明了G具有一個“泛”覆蓋群G,使得G的每一覆蓋群是G的同態像.而Z(G)恰為G的舒爾乘子.
