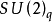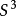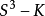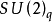歐氏空間R3中的簡單閉曲線稱為扭結(knot)。由有限條直線所組成的扭結稱為多邊形扭結。設K1和K2是扭結,如果存在同胚h: R3→R3,使得h(K1)=K2,則稱它們是等價的;如果存在恆同映射的同倫H:R3×[0,1]→R3,使得對每個t∈[0,1],ht=H(·,t):R3→R3是保持定向的同胚,且h1(K1)=K2,則稱K1和K2有相同的痕型。直觀上,K1和K2有相同的痕型是指K1可連續地形變成K2,且在形變過程中不自身相交。痕型相同的扭結必定等價。扭結理論的中心問題是按等價或痕型將扭結分類,並求出相應的不變數。設K是扭結,R3-K的基本群稱為扭結群,等價(同痕型)的扭結有同構的扭結群。對於多邊形扭結,利用馮坎本定理可求得其扭結群。圓周的扭結群同構於Z,三葉扭結的扭結群不與Z同構,因此圓周與三葉扭結不等價。
基本介紹
- 中文名:扭結群
- 外文名:knot group
- 所屬學科:數學
- 相關概念:扭結,馮坎本定理等
基本介紹,相關概念介紹,
基本介紹
扭結群(knot group)是研究扭結的一個工具。若K為扭結,則 的基本群
的基本群 稱為K的扭結群。取扭結K的一個正則投影P,使得投影平面為
稱為K的扭結群。取扭結K的一個正則投影P,使得投影平面為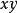 平面,然後對於
平面,然後對於 中的每個二重點P,設它對應於K中的兩個點
中的每個二重點P,設它對應於K中的兩個點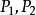 ,這時,若
,這時,若 的z坐標大於
的z坐標大於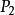 的z坐標,則稱K中
的z坐標,則稱K中 附近線段的投影為
附近線段的投影為 中的上行段,
中的上行段,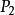 附近線段的投影為
附近線段的投影為 中的下行段(如圖)。若給定K的一個指向,選取
中的下行段(如圖)。若給定K的一個指向,選取 的基點為z坐標充分大的點q,對於每條上行段,引入一條以q為基點的環道,它對於K的指定的取向右旋的繞上行段一周,這些環道在
的基點為z坐標充分大的點q,對於每條上行段,引入一條以q為基點的環道,它對於K的指定的取向右旋的繞上行段一周,這些環道在 中所決定的元素記為
中所決定的元素記為 (
(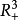 表示R的上半空間),然後對於每個交點,如圖所示,引入關係
表示R的上半空間),然後對於每個交點,如圖所示,引入關係 ,則K的扭結群
,則K的扭結群


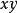

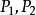

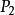


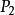




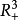





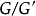
相關概念介紹
扭結(knot)亦稱環繞,是幾何拓撲學的一個重要概念。設K是拓撲空間X的一個子集,若K同胚於p維球面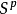 ,則稱K為X中的一個扭結。一般地,X的一個子集K,若K同胚於r個球面的無交並
,則稱K為X中的一個扭結。一般地,X的一個子集K,若K同胚於r個球面的無交並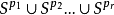 ,則稱為X中的一個環繞。所以扭結是環繞的特殊情形,對於X中的兩個扭結或環繞
,則稱為X中的一個環繞。所以扭結是環繞的特殊情形,對於X中的兩個扭結或環繞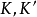 ,若存在同胚
,若存在同胚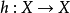 ,使得
,使得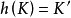 ,即
,即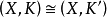 ,則稱為等價的。扭結或環繞的等價類稱為扭結型或環繞型。實際上,除了有特別的說明以外,在這些問題中,一般總假定X為n維歐氏空間,n維球面或n維單形,在這裡限制X為3維歐氏空間
,則稱為等價的。扭結或環繞的等價類稱為扭結型或環繞型。實際上,除了有特別的說明以外,在這些問題中,一般總假定X為n維歐氏空間,n維球面或n維單形,在這裡限制X為3維歐氏空間 ,K為
,K為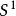 ,即此處所指的扭結是
,即此處所指的扭結是 中的一條簡單閉曲線。對於
中的一條簡單閉曲線。對於 的一個自同胚h,若存在倫移
的一個自同胚h,若存在倫移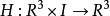 ,使得每個
,使得每個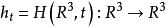 為同胚,
為同胚,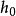 為恆等映射,
為恆等映射,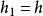 ,則稱為合痕於恆等映射。對於
,則稱為合痕於恆等映射。對於 中的扭結
中的扭結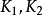 若存在
若存在 的合痕
的合痕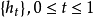 ,使得
,使得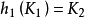 ,則稱
,則稱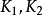 有相同的合痕型。合痕與等價是兩個不同的概念。例如,圖中所列的兩個三瓣扭結是等價的,但不具有相同的合痕型,因為
有相同的合痕型。合痕與等價是兩個不同的概念。例如,圖中所列的兩個三瓣扭結是等價的,但不具有相同的合痕型,因為 關於其中某張平面的反射,可把
關於其中某張平面的反射,可把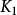 變為它的鏡面像
變為它的鏡面像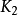 ,但不能通過連續的變形把
,但不能通過連續的變形把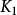 變為
變為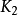 。
。 到自身的同胚可以惟一地擴張為
到自身的同胚可以惟一地擴張為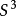 到自身的同胚,因此在討論扭結問題時,也可用
到自身的同胚,因此在討論扭結問題時,也可用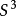 代替
代替 ,於是可知任意同胚
,於是可知任意同胚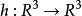 合痕於恆等同胚若且唯若h為保向同胚。
合痕於恆等同胚若且唯若h為保向同胚。 中
中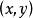 平面上的單位圓周所表示的扭結及其扭結型稱為平凡的或不打結的,否則稱為打結的。在扭結的等價之下,可用
平面上的單位圓周所表示的扭結及其扭結型稱為平凡的或不打結的,否則稱為打結的。在扭結的等價之下,可用 中由有限條邊構成的多邊形來表示的扭結稱為溫良的,否則稱為野生的。對於可用多邊形表示的溫良扭結K,可取
中由有限條邊構成的多邊形來表示的扭結稱為溫良的,否則稱為野生的。對於可用多邊形表示的溫良扭結K,可取 中的平面
中的平面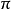 以及
以及 到π的投影p,使得:
到π的投影p,使得:
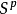
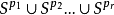
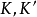
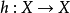
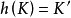
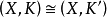

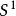


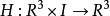
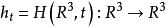
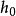
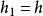

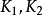

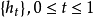
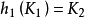
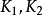

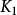
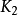
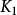
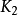

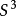
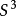





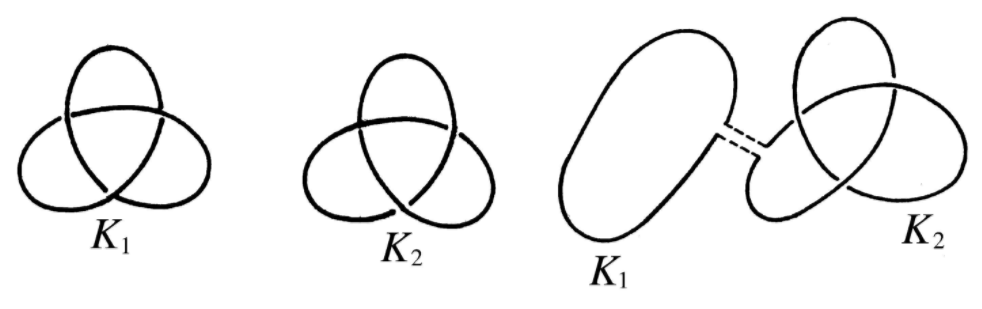 圖1
圖11.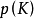 的多重點只限於二重點,並且只有有限個。
的多重點只限於二重點,並且只有有限個。
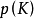
2.K的頂點不映為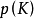 的二重點,這樣的一個投影稱為K的正則投影。
的二重點,這樣的一個投影稱為K的正則投影。
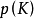
若兩個紐結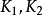 處於互不相繞的位置,則可以通過兩段小弧把它們互相連結起來,如同上圖右,這樣形成的一個新扭結稱為扭結
處於互不相繞的位置,則可以通過兩段小弧把它們互相連結起來,如同上圖右,這樣形成的一個新扭結稱為扭結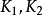 的結合,結合的操作稱為扭結的乘法。於是全體扭結型在這種乘法之下成為一個交換半群。一個扭結型稱為素的,若不能再用非平凡扭結將它分解。所以在此扭結型半群之中,每一個扭結型能惟一地表示成有限個素扭結型的乘積。
的結合,結合的操作稱為扭結的乘法。於是全體扭結型在這種乘法之下成為一個交換半群。一個扭結型稱為素的,若不能再用非平凡扭結將它分解。所以在此扭結型半群之中,每一個扭結型能惟一地表示成有限個素扭結型的乘積。
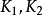
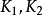
在20世紀30年代之前,扭結理論主要以美國的亞歷山大(Alexander,J.W.)以及德國的賴德邁斯特(Reidemeister,K.W.F.)、賽費特(Seifert,H.K.I.)為代表發展起來的,40年代幾乎沒有太多進展.以後,美國的福克斯(Fox,R.H.)在這方面的貢獻較多。進入20世紀80年代以來,一些著名數學家如韋吞(Witten,E.)等投入這方面研究,他把扭結理論與量子場聯繫起來,得到了瓊斯-韋吞(Jones-Witten)的不變數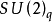 。高登(Gordon,C.M.)與呂克(Luecker,J.)證明了
。高登(Gordon,C.M.)與呂克(Luecker,J.)證明了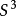 中的一個扭結K由它的補
中的一個扭結K由它的補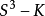 決定。里可里西(Lickorish)利用考夫曼(Kauffmen)括弧多項式構造了3維流形不變數,並描述此不變數與
決定。里可里西(Lickorish)利用考夫曼(Kauffmen)括弧多項式構造了3維流形不變數,並描述此不變數與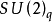 的關係。
的關係。