扭群((twisted group)謝瓦萊群的重要子群.設單李代數L=Ar,DZ,E6,B2,G:或L "l4,它的鄧金圖有非平凡的對稱P}P的階n=2或3.設K是域,且當1.=BZ或F、時K是特徵2的完全域;當L=GZ時K是特徵3的完全域,若G=L(K)是K上L型謝瓦萊群,則存在G的自同構g,稱為圖自同構,將每個基礎根aEll對應的根子群X。變為基礎根p(a)對應的根子群}'}ca>.域K的每個自同構:也決定G的一個自同構,稱為域自同構並仍記為:,將每個根元素x,Ct)變為二:(t`>.圖自同構g與每個域自同構:相交換,它們的乘積。一g:仍是G的自同構.選取非平凡的域自同構:使。一g:與p具有相同的階n,即a" = 1.所有的正根rE}+對應的根子群X,生成G的子群U,所有的負根rE}一對應的根子群X,生成子群Y.又,若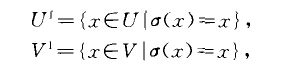
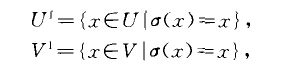
則U,與Y’生成的子群記為”L(K>,稱為扭群.
