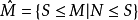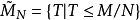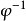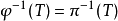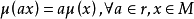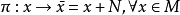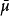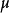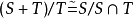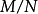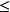模同構是一種特殊的模同態,假設f是模M到模N的同態,若f時一一的並且是映上的,則f為模M到模N的同構。兩個同構的模,從模的結構來看,它們沒有什麼區別。模同構具有一個性質,即若f為模M到模N的同態,則f的逆映射f^(-1)也是同構。廣義模同構是一種廣義模同態。
基本介紹
- 中文名:模同構
- 外文名:module isomorphism
- 基礎:模同態
- 推廣:廣義模同構
- 重點:三個模同構定理
- 套用學科:基礎代數
預備知識,模的同態映射,模的分解定理,定義介紹,模的同構定理,模的對應定理,定理1,定理2,
預備知識
模的同態映射
模的分解定理
設映射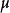 為M 到M' 的一個模同態(M,H 為兩個R -模)。則分解式
為M 到M' 的一個模同態(M,H 為兩個R -模)。則分解式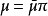 成立,知:
成立,知:
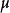
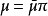
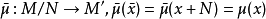
(1)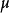 為滿模同態若且唯若
為滿模同態若且唯若 為滿同態;
為滿同態;
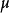

(2)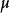 為單模同態若且唯若
為單模同態若且唯若 ;
;
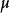

(3) 為模同構若且唯若為
為模同構若且唯若為 滿同態,且
滿同態,且 。
。



定義介紹
模同構(module isomorphism)是一種特殊的模同態,模M到N的同態f若是一一的並且是映上的,則稱f是M到N 的同構,這時稱M,N 是同構的模,記為M=N 。兩個同構的模,從模的結構來看,它們沒有什麼區別。若f 是同構,則f 的逆映射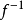 也是同構。
也是同構。
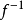
廣義模同構是一種廣義模同態。設A,B 是k-代數,且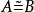 ,M 是A 上的模,N 是B 上的模,M 到N 的k-線性映射
,M 是A 上的模,N 是B 上的模,M 到N 的k-線性映射 如果滿足
如果滿足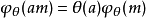 ,則稱
,則稱 為
為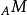 到
到 的廣義模同態;特別的,如果
的廣義模同態;特別的,如果 是雙射,則
是雙射,則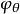 稱為
稱為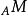 到
到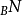 的廣義模同構,記作
的廣義模同構,記作 。
。
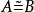

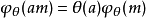

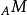


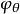
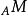
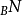

模的同構定理
模的第一同構定理
設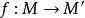 為模同態,且
為模同態,且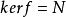 ,那么
,那么 。
。
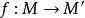
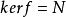

注意:在證明的過程中運用分解定理,同時需要注意 為到
為到 上的一個滿同態映射。
上的一個滿同態映射。


模的第二同構定理
證明:直接驗證不難知道,S+T 和S∩T 均為M 的子模。
定義映射 ,那么映射f 為模同態,其同態核kerf=S∩T ,它的同態像為
,那么映射f 為模同態,其同態核kerf=S∩T ,它的同態像為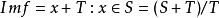 ,從而由第一同構定理知結論成立。
,從而由第一同構定理知結論成立。

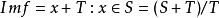
模的第三同構定理
設N≤L≤M (即N 為L 的子模,L 為M 的子模),那么 。
。

證明:定義映射 ,
,

則有: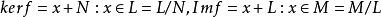 。
。
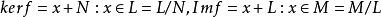
再由第一同構定理知結論成立。
模的對應定理
定理1
設N 為一個R -模M 的一個子集,記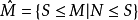 以及
以及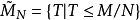 ,即
,即 為M 的所有包含N 的子模的集合,
為M 的所有包含N 的子模的集合, 為M/N 的所有子模的集合。則映射
為M/N 的所有子模的集合。則映射 為
為 到
到 的一個1-1對應。其逆映射
的一個1-1對應。其逆映射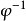 滿足
滿足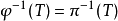 ,這裡
,這裡 為M 到M/N 的自然模同態。
為M 到M/N 的自然模同態。