子模(submodule)是模論的重要概念之一,指A模M滿足一定條件的子集。定義:設M是一個R - 模,A是M的一個子集,如果A對於M的加法和M與R的數乘來說也構成一個R - 模,則稱A是M的一個子模,M稱為A的擴模。
基本介紹
- 中文名:子模
- 外文名:submodule
- 定義:A模M滿足一定條件的子集
- 包含:極大子模、極小子模等
- 一級學科:數學
- 二級學科:模論
定義
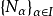

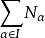
分類
極大子模
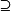
極小子模
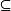
本質子模
多餘子模
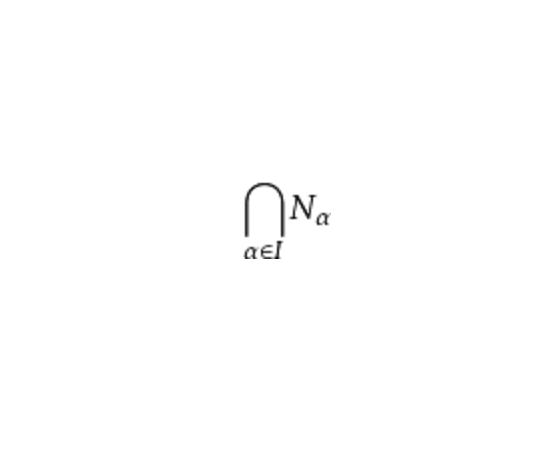
子模(submodule)是模論的重要概念之一,指A模M滿足一定條件的子集。定義:設M是一個R - 模,A是M的一個子集,如果A對於M的加法和M與R的數乘來說也構成一個R - 模,則稱A是M的一個子模,M稱為A的擴模。
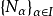

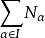
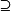
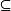
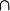
子模(submodule)是模論的重要概念之一,指A模M滿足一定條件的子集。定義:設M是一個R - 模,A是M的一個子集,如果A對於M的加法和M與R的數乘來說也構成一...
介紹 極大子模(maximal submodule)一類重要子模.若N是A模M的真子模,並且不存在嚴格包含N的M的真子模(即,若N'是M的真子模,且N'?N,則一定有N' = N成立...
由拼組的於模組複製成的印版,若其中某一子模發生缺損,則以備用的於模替換缺損的於模,為子模替代。 ...
定義介紹 多餘子模(superfluous submodule)亦稱小子模一類重要的子模.本質子模的對偶概念.設K是A模M的子模,若對M的子模L,由K-}L=M可斷言1=M,則稱K為M的...
穩定子模(stable submodule)不變子空間概念的推廣。...... 穩定子模(stable submodule)不變子空間概念的推廣。設M是A模,f:M->M是A同態,N是M的一個子模,若...
花拉子模州(烏茲別克語:Khwarazm viloyati)是烏茲別克斯坦十二個州份之一。它涵蓋6,300平方公里,有人口1,200,000。花拉子模州下轄10個縣,首府設於烏爾根奇市。...
定義 極小子模(minimal submodule)與極大子模是互為對偶的概念.若N是A模M的子模,並且不存在嚴格包含在N內的M的非零子模(即,若N'是M的非零子模,且N' ...
凸L子模(convex L-submodule)一類重要的子模.設MR是環R上的格模,N是M的R子模.若N是M的凸l子群,則稱N為M的凸L子模.若M/N是全序的,則N稱為M的...
全不變子模(fully invariant submodule)一類特殊的穩定子模.設N是模M的子模,若N對模的任一個自同態都穩定,則稱N是M的一個全不變子模.模M是擬內射模的...
花拉子模沙三王朝(KhwārezmShāhs,three dynasties of),10~13世紀中亞歷史上先後存在過的3個伊斯蘭教花拉子模沙王朝。...
用母模翻壓複製子模時加上的暗記,稱子模暗記。乾模暗記不是在每枚郵票中部能找到,在全張郵票中往往只有幾枚有暗記。 ...
張子模,男,1953年2月出生,漢族,廣西興安人,現任桂林市園林局黨組副書記、副局長。中文名 張子模 民族 漢族 出生地 廣西興安 出生日期 1953年2月 ...
郵票印版是由幾塊或幾十塊單枚子模拼排而成,整塊印版排用的子模數即為子模數量,如清代“大龍”票印版是由25塊魚枚子模(5X 5=25)拼排而成,其子模數量...
定義 本質子模(essential submodule)亦稱大子模一類重要的子模.它是在一定程度上可代替模本身的子模,是多餘子模的對偶概念.設K是A模M的子模,若對M的子模I,...
奇異子模(singular submodule)一類重要的子模.它是關於本質理想零化的子模.設M是右A模,若Z(M)一{二EM}xI=0,對A的某本質右理想I},則Z(M)是M的一個子...
拼版時誤將另一種郵票的子模植入,造成在一個印版中出現另一種郵票的子模。如區票廣化版毛主席像普通郵票,曾產生過子模誤值情況,在50元票(紅色)印版中,誤...
趙子模(1925年-1949年5月),男,江西省南豐人。 生前是一名地下工作者。中文名 趙子模 出生日期 1925年 逝世日期 1949年5月 性別 男 籍貫 江西省南豐 ...
次模函式是一個集合函式,隨著輸入集合中元素的增加,增加單個元素到輸入集合導致的函式增量的差異減小。 次模函式具有單調遞減的特性,使得它們適用於許多套用,包括近似...
定義介紹 撓模(torsion module)一類重要的模.撓群的推廣.設M是A模,若對。}mEM,有。}aEA,使得am=0成立,則稱m是,M的撓元.當A為整環時,,, M中所有的撓...
摩訶末即穆罕默德,漢文古譯。1200年,阿拉烏丁·摩訶末即位,仍向西遼稱臣。他的第一次戰爭是與阿富汗的古爾王朝開戰。第一仗在阿姆河畔,阿富汗前往掠奪花剌子模,在...
