若同態映射 f 是一個雙射,則稱 f 為 G 到 G’ 的同構映射,這時稱群 G 和 G’ 同構。
基本介紹
- 中文名:同構映射
- 外文名:homomorphis of group
- 適用領域:數學群論
- 相關概念:同構;同態映射
簡介

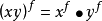
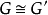
同構
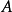
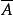



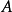
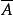



 圖1.
圖1.若同態映射 f 是一個雙射,則稱 f 為 G 到 G’ 的同構映射,這時稱群 G 和 G’ 同構。

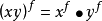
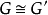
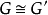
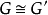
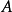
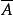



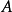
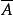



 圖1.
圖1.若同態映射 f 是一個雙射,則稱 f 為 G 到 G’ 的同構映射,這時稱群 G 和 G’ 同構。...
在抽象代數(abstract algebra)中,同構(isomorphism)指的是一個保持結構的雙射(bijection)。在更一般的範疇論語言中,同構指的是一個態射,且存在另一個態射,使得...
同構證明方法是一種證明方法。同態和同構是布爾巴基學派提出的重要概念,它是對於結構之間關係的描述。雖然同構概念提出較晚,但其意義是極其深遠的。同構不僅是數學的...
同態與同構,是近世代數系統中的概念,是學習其他相關課程的基礎概念。...... *>和<S, °>,如果f是從G到S的一個雙射,則稱f是從G到S的同構映射,G與S同構,...
設X,Y是兩個賦范線性空間,U是X到Y的映射,若對一切x∈X,有||Ux||=||x||,則稱U是保范映射或等距映射。...
半線性映射(semi-linear mapping)是線性映射概念的推廣。線性映射亦稱同態或線性同態。線性代數的中心內容和基本概念之一。線性空間亦稱向量空間。它是線性代數的中心...
若兩個測度環之間存在一個同構映射,則說明這兩個測度環是同構的,即為同構測度環。...... 若兩個測度環之間存在一個同構映射,則說明這兩個測度環是同構的,即為...
雙全純映射是有逆映射的全純映射。雙全純映射中,f(D)為Cn中的域,並稱D和f(D)互相全純同構。...
擬同構是同調代數中的一個概念,具體定義請參見正文,擬同構給出導出範疇中的同構。...... 若兩個數學結構之間存在同構映射,那么這兩個結構叫做是同構的。一般來說...
描述 模型同構(isomorphism of models)模型論術語.指兩模型間的一種等價關係.語言丫中的模型}l=CA,{r},}f},{:})和.}= CB,{、},fig},{d})同構(記為...
同構測度空間(measure space of isomorphim)是指其連帶的測度環同構的測度空間。...... 則稱T是(Ω1,μ)和(Ω2,v)之間的同構映射。若兩個測度環之間存在一...
有理映射是代數簇上的有理函式概念的推廣。但是,它並不是集合意義下的映射。代數簇是代數幾何的基本研究對象。設k是一個域,域k上的代數簇就是一個整的、分離...
模同構是一種特殊的模同態,假設f是模M到模N的同態,若f時一一的並且是映上的,則f為模M到模N的同構。兩個同構的模,從模的結構來看,它們沒有什麼區別。模...
