基本介紹
- 中文名:球面三角學
- 外文名:spherical trigonometry
- 領域:幾何學
- 主要解決:三角形問題
- 主要量:球面角,球面三角形
- 套用領域:測量學,天文學和航海等
球面上的線
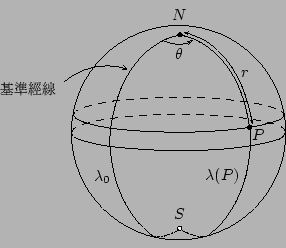 圖1.球面三角
圖1.球面三角
球面三角形
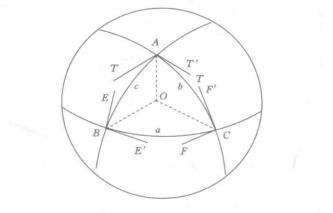 圖2.球面三角形
圖2.球面三角形



球面角超







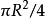



球面公式

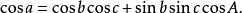






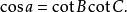
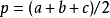



 圖1.球面三角
圖1.球面三角
 圖2.球面三角形
圖2.球面三角形










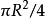




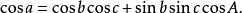






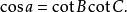
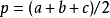



球面三角學是球面幾何學的一部分,主要在處理、發現和解釋多邊形 (特別是三角形) 在球面上的角與邊的聯繫和關聯。在天文學上的重要性是用於計算天體軌道和地球表面...
三角學是指以研究平面三角形和球面三角形的邊和角的關係為基礎,達到測量上的套用為目的一門學科。同時,三角學還研究三角函式的性質以及它們的套用。...
球面幾何學是在二維的球面表面上的幾何學,也是非歐幾何的一個例子。...... 球面三角學是球面幾何學的一部分,主要在處理、發現和解釋多邊形(特別是三角形) 在球面...
球面三角是研究球面三角形的邊、角關係的一門學科。從十六世紀起由於天文學、航海學、測量學等方面的發展,球面三角逐漸形成了獨立學科。從平面三角學我們知道,一...
球面天文學,天體測量學的一個分支,主要內容是運用球面三角學和矩陣運算等數學方法研究投影在天球上的天體位置及其因大氣折射和地球運動等引起的變化。球面天文學是...
然而古希臘的三角學基本是球面三角學。這與古希臘人研究的主體是天文學有關。梅涅勞斯在他的著作《球面學》中使用了正弦來描述球面的梅涅勞斯定理。古希臘三角學與其...
在球面上,最短線是大圓的弧,所以平面幾何中的線在球面幾何中被大圓所取代。同樣的,在球面幾何中的角被定義在兩個大圓之間。結果是球面三角學和平常的三角學有...
球面天文學研究方法是利用在天球上建立的天球坐標系研究天體投影在天球上的位置以及由於各種因素而產生的位置移動的科學方法。是天體測量學、天體力學、星系動力學及...
旁鄰球面三角形是一種特殊的球面三角形,指給定球面三角形的兩個頂點和第三個頂點的對徑點所構成的球面三角形。...
梅涅勞斯在他的著作《球面學》中使用了正弦來描述球面的梅涅勞斯定理。古希臘三角學與其天文學的套用在埃及的托勒密時代達到了高峰,托勒密在《數學彙編》(Syntaxis ...
公元1464年 德國J.雷格蒙塔努斯(Johannes Regiomo,1436-1476)著《論各種三角形》(De triangulis omni-modis)。他曾就學於萊比錫,後到奧地利維也納深造,學習天文學...
對心球面三角形(oppositely central sphericaltriangle)亦稱對頂球面三角形.兩個位置相關的球面三角形。指三個頂點分別互為對徑點的兩個球面三角形.對心球面三角形...
