基本介紹
- 中文名:正弦公式
- 外文名:Sine Law
- 別稱:正弦定理
- 描述:各邊和它所對角的正弦的比相等
- 套用領域:幾何學
定義
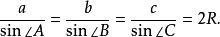
公式證明
1.證明一
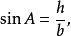




2.證明二
 圖2.餘弦公式證明-銳角時
圖2.餘弦公式證明-銳角時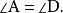

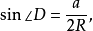


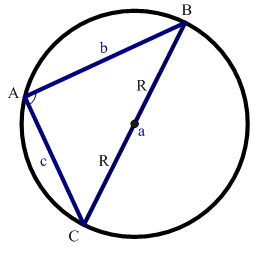 圖3.餘弦公式證明-直角時
圖3.餘弦公式證明-直角時
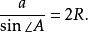

 圖4.餘弦公式證明-鈍角時
圖4.餘弦公式證明-鈍角時

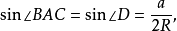

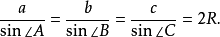
意義
公式套用
1.三面角正弦定理

2.多邊形的正弦關係
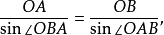

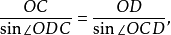

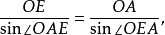
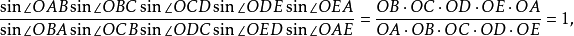
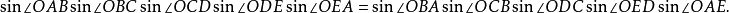
 圖6.多邊形的正弦關係
圖6.多邊形的正弦關係
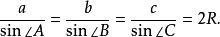
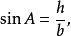




 圖2.餘弦公式證明-銳角時
圖2.餘弦公式證明-銳角時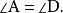

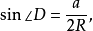


 圖3.餘弦公式證明-直角時
圖3.餘弦公式證明-直角時
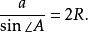

 圖4.餘弦公式證明-鈍角時
圖4.餘弦公式證明-鈍角時

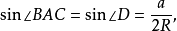

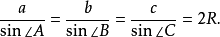

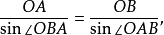

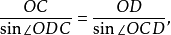

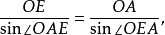
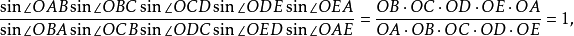
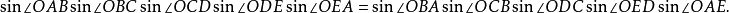
 圖6.多邊形的正弦關係
圖6.多邊形的正弦關係正弦公式是描述正弦定理的相關公式,而正弦定理是三角學中的一個基本定理,它指出:在任意一個平面三角形中,各邊和它所對角的正弦值的比相等且等於外接圓的直徑。...
以誘導公式四為例: 若將α看成銳角(終邊在第一象限),則π-α是第二象限的角(終邊在第二象限),正弦函式的三角函式值在第二象限是正值,餘弦函式的三角函式值...
正弦定理(The Law of Sines)是三角學中的一個基本定理,它指出“在任意一個平面三角形中,各邊和它所對角的正弦值的比相等且等於外接圓的直徑”,即a/sinA = ...
正弦(sine),數學術語,在直角三角形中,任意一銳角∠A的對邊與斜邊的比叫做∠A的正弦,記作sinA(由英語sine一詞簡寫得來),即sinA=∠A的對邊/斜邊。古代說法,...
正弦曲線或正弦波(Sinusoid/Sine wave)是一種來自數學三角函式中的正弦比例的曲線。也是模擬信號的代表,與代表數位訊號的方波相對。正弦曲線可表示為y=Asin(ωx+φ...
正弦值是在直角三角形中,對邊的長比上斜邊的長的值。 任意銳角的正弦值等於它的餘角的餘弦值,任意銳角的餘弦值等於它的餘角的正弦值。...
兩角和(差)公式包括兩角和差的正弦公式、兩角和差的餘弦公式、兩角和差的正切公式。兩角和與差的公式是三角函式恆等變換的基礎,其他三角函式公式都是在此公式基礎...
公式(1)(sinα)^2+(cosα)^2=1(2)1+(tanα)^2=(secα)^2(3)1+(cotα)^2=(cscα)^2證明下面兩式,只需將一式,左右同除(sinα)^2,第二個...
正弦電流(sine-wave current)指按正弦規律隨時間變化的交變電流,工程上常用正弦電流和電壓的有效值表示其大小。...
正弦積分是由積分定義的一種特殊函式。英文翻譯為sine integral,常用語計算正弦積分函式值,在性質上常與餘弦積分作比較。...
數學公式是人們在研究自然界物與物之間時發現的一些聯繫,並通過一定的方式表達出來的一種表達方法。是表征自然界不同事物之數量之間的或等或不等的聯繫,它確切的...
數學中,泰勒公式是一個用函式在某點的信息描述其附近取值的公式。如果函式足夠平滑的話,在已知函式在某一點的各階導數值的情況之下,泰勒公式可以用這些導數值做...
在直角三角形中,∠α(不是直角)的對邊與斜邊的比叫做∠α的正弦,記作sinα,即sinα=∠α的對邊/∠α的斜邊 。sinα在拉丁文中記做sinus。在古代的說法當...
一般地,把三角形的三個角A,B,C和它們的對邊a,b,c叫做三角形的元素。已知三角形的幾個元素求其他元素的過程叫做解三角形。解三角形,常用到正弦定理和餘弦定理...
