基本介紹
- 中文名:棣莫弗定理
- 外文名:De Moivre's formula
- 表達式:Z1Z2=r1r2[cos(θ1+θ2)+isin(θ1+θ2)]
- 提出者:棣莫弗
- 套用學科:數學
- 適用領域範圍:複數
- 相關公式:歐拉公式
科學原理


定理證明



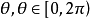





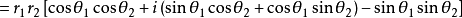

推廣形式
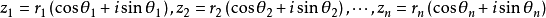

乘方形式
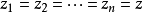
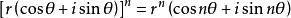
乘方形式證明
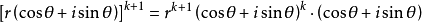

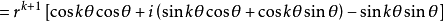

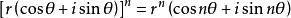
與歐拉公式的聯繫


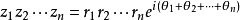

棣莫佛定理一般指本詞條





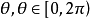





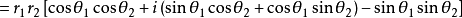

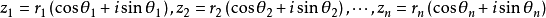

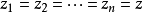
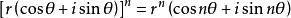
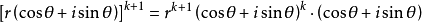

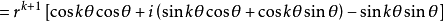

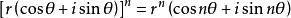


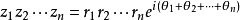
棣莫弗定理由法國數學家棣莫弗(1667-1754年)創立。指的是設兩個複數(用三角函式形式表示)Z1=r1(cosθ1+isinθ1),Z2=r2(cosθ2+isinθ2),則:Z1Z2=...
棣莫佛(De moivre, 1667~1754)於1667年出生於法國香檳,長大後在巴黎從師學習數學。由於宗教信仰的緣故,十八歲那年他被迫離開自己的祖國,去了英國倫敦。在那裡,...
▪ 定理 棣莫弗人物簡介 編輯 亞伯拉罕·棣莫弗,1667年5月26日生於法國維特里的弗朗索瓦;1754年11月27日卒於英國倫敦.棣莫弗出生於法國的一個鄉村醫生之家,...
棣莫弗—拉普拉斯中心極限定理(De Moivre-Laplace),即二項分布以常態分配為其極限分布定律。...
棣莫弗一拉普拉斯局部極限定理(De Moivre-Laplace local limit theorem)是關於伯努利試驗的極限定理。伯努利試驗(Bernoulli experiment)是在同樣的條件下重複地、相互...
棣莫弗,A·,男,法國人,生於1667年 5月26日,卒於1754年11月27日,1718年出版《機遇論》,這是早期機率論的重要著作,其中第一次定義獨立事件的乘法定理。1733...
亞伯拉罕·棣莫弗(Abraham De Moivre;法國裔英國籍的數學家,1667年5月26日生...這是機率論較早的專著之一,首次定義了獨立事件(Independent Event)的乘法定理,...
法國數學家棣莫弗(1667—1754)在1722年發現了著名的棣莫佛定理。歐拉在1748年發現了有名的關係式,並且是他在《微分公式》(1777年)一文中第一次用i來表示-1...
“常態分布”,又名高斯分布(Gaussian distribution),最早由A.棣莫弗在求二項...常態分配定理 編輯 由於一般的正態總體其圖像不一定關於y軸對稱,對於任一正態...
推導過程:棣莫佛公式:n=4代入得 ,左邊用二項式定理展開可得根據複數相等的充要條件分子分母同除以(cosx)^4並化簡得詞條標籤: 科學 ...
此即複平面上的棣莫佛定理,在這裡成為了三元數乘方的一個特例。2.三元數的開方三元數的n次方根是r^1/n[(cos(θ+2kπ)/n)+sin((θ+2kπ)/n)(icosφ...
指數微積分/負數的對數/聖彼得堡悖論/亞伯拉罕·棣莫弗/棣莫弗定理/羅傑·科茨/詹姆斯·斯特林/科林·麥克勞林/泰勒級數/《分析學家》論戰/克萊姆法則/契恩豪斯變換...
此外,他於1695年寫過研究牛頓流數法的論文;1707年在研究三角學時實質上已得到「棣莫弗定理」(De Moivre's Theorem),(cos x + i sin x)n = cos nx + ...
1. 在複平面(即高斯平面)上,單位圓誘導了著名的歐拉公式和棣莫佛定理。 換句話說, 單位圓上的點表示模長為1的複數, 它誘導了複數的三角形式和指數形式之間的...
複數的指數形式,歐拉公式,棣莫佛定理,單位根,單位根的套用。圓排列,有重複的排列與組合,簡單的組合恆等式。一元n次方程(多項式)根的個數,根與係數的關係,實...
複數的指數形式,歐拉公式,棣莫佛定理,單位根,單位根的套用。圓排列,有重複的排列與組合,簡單的組合恆等式。一元n次方程(多項式)根的個數,根與係數的關係,實...
§5.3 中心極限定理5.3.1 獨立同分布序列的中心極限定理5.3.2 棣莫弗(DeMoivre)-拉普拉斯( Laplace)中心極限定理習題5.3小結...
指數微積分/負數的對數/聖彼得堡悖論/亞伯拉罕·棣莫弗/棣莫弗定理/羅傑·科茨/詹姆斯·斯特林/科林·麥克勞林/泰勒級數/《分析學家》論戰/克萊姆法則/契恩豪斯變換...
棣莫佛定理 複數的三角形式的除法 複數的三角形式的開方 負實數的平方根 實數係數一元二次方程虛根 成對定理 二項方程 八 排列、組和與 二項式定理 加法原理 ...
