基本介紹
- 中文名:多面體歐拉定理
- 別稱:歐拉定理
- 表達式:V-E+F=2
- 提出者:歐拉
- 套用學科:數學
- 適用領域範圍:頂點數V、棱數E及面數F
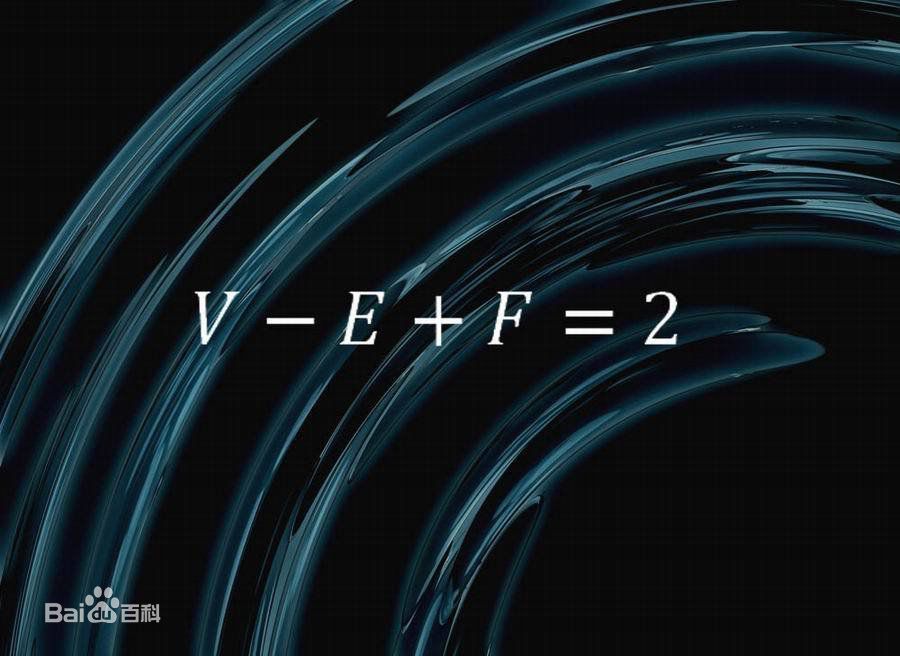
多面體歐拉定理是指對於簡單多面體,其頂點數V、棱數E及面數F間有著名的歐拉公式:V-E+F=2。簡單多面體即表面經過連續變形可以變為球面的多面體。...
歐拉發現,不論什麼形狀的凸多面體,其頂點數V、棱數E、面數F之間總有關係V+F-E=2,此式稱為歐拉公式。V+F-E即歐拉示性數,已成為“拓撲學”的基礎概念。...
在任何一個規則球面地圖上,用 R記區域個 數,V記頂點個數 ,E記邊界個數 ,則 R+ V- E= 2,這就是歐拉定理 ,它於 1640年由 Descartes首先給出證明 ,後來...
歐拉定理證明“用‘嵌入’ 法中和” 編輯 7 和上一法不同, 我們首先得到凸多面體的在二維平面的一個 "嵌入"(embedding) :如圖: 首先, 我們旋轉圖使之沒有一...
由歐拉定理可知一共只有這5種正多面體。 [1] 有兩個面互相平行,其餘各面都是四邊形,並且每相鄰兩個四邊形的公共邊都互相平行的多面體叫做稜柱(如圖1)。兩個...
歐拉定理實際上是費馬小定理的推廣。此外還有平面幾何中的歐拉定理、多面體歐拉定理(在一凸多面體中,頂點數-棱邊數+面數=2)。西方經濟學中歐拉定理又稱為產量分配...
凸多面體各個頂點的欠角的和恆等於720度 (可以使用歐拉定理證明)。...... 凸多面體各個頂點的欠角 [1] 的和恆等於720度 (可以使用歐拉定理 [2] 證明)。...
對於正多面體,且對於零類多面體,歐拉定理成立: ,其中B——頂點數, ——面數,p——多面體的棱數。正四面體 正六面體 正八面體 正十二面體 正二十面體...
由“歐拉定理”可以推出正多面體只有正四面體、正六面體、正八面體、正十二面體、正二十面體五種。也正因為正多面體的特性,所以由正多面體骰子得到的隨機數可能性...
那么,該多面體的面數F=7(定義)。因為兩個面交於一棱,所以棱數E=7m/2。因為n條棱交於一頂點,所以頂點數V=2E/n=7m/n。根據歐拉公式,V+F-E=2,所以7m/...
後來在拓撲學的形成中占著重要的地位。譬如哥尼斯堡七橋問題、多面體的歐拉定理、四色問題等都是拓撲學發展史的重要問題。拓撲學七橋問題 ...
在拓撲學的發展歷史中,還有一個著名而且重要的關於多面體的定理也和歐拉有關。這個定理內容是:如果一個凸多面體的頂點數是v、棱數是e、面數是f,那么它們總有...
這個定理內容是:如果一個凸多面體的頂點數是v、棱數是e、面數是f,那么它們總有這樣的關係:f+v-e=2。根據多面體的歐拉定理,可以得出這樣一個有趣的事實:只...
在拓撲學的發展歷史中,還有一個著名而且重要的關於多面體的定理也和歐拉有關。這個定理內容是:如果一個凸多面體的頂點數是v、棱數是e、面數是f,那么它們總有...
