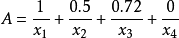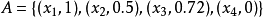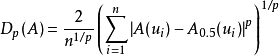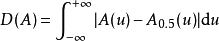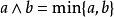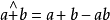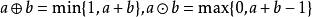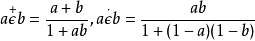模糊集合

模糊集合是用來表達模糊性概念的集合。 又稱模糊集、模糊子集。普通的集合是指具有某種屬性的對象的全體。

1965年美國學者扎德在數學上創立了一種描述模糊現象的方法—模糊集合論。這種方法把待考察的對象及反映它的模糊概念作為一定的模糊集合，建立適當的隸屬函式，通過模糊集合的有關運算和變換，對模糊對象進行分析。模糊集合論以模糊數學為基礎，研究有關非精確的現象。客觀世界中，大量存在著許多亦此亦彼的模糊現象。

基本介紹

• 中文名：模糊集合
• 外文名：fuzzy set
• 又名：模糊集、模糊子集
• 提出人物：L.A.扎德
• 提出時間：1965
• 套用學科：數學

定義

這種屬性所表達的概念應該是清晰的，界限分明的。因此每個對象對於集合的隸屬關係也是明確的，非此即彼。但在人們的思維中還有著許多模糊的概念，例如年輕、很大、暖和、傍晚等，這些概念所描述的對象屬性不能簡單地用“是”或“否”來回答，模糊集合就是指具有某個模糊概念所描述的屬性的對象的全體。由於概念本身不是清晰的、界限分明的，因而對象對集合的隸屬關係也不是明確的、非此即彼的。這一概念是美國加利福尼亞大學控制論專家L.A.扎德於 1965 年首先提出的。模糊集合這一概念的出現使得數學的思維和方法可以用於處理模糊性現象，從而構成了模糊集合論（中國通常稱為模糊性數學)的基礎。

給定一個論域U，那么從U到單位區間 [0,1] 的一個映射 稱為U上的一個模糊集，或U的一個模糊子集。

表示

模糊集可以記為A。 映射（函式）μ_A(·) 或簡記為A(·) 叫做模糊集A的隸屬函式。 對於每個x∈U，μ_A(x) 叫做元素x對模糊集A的隸屬度。

模糊集的常用表示法有下述幾種：

（1）解析法，也即給出隸屬函式的具體表達式。

（2）Zadeh 記法，例如 。分母是論域中的元素，分子是該元素對應的隸屬度。有時候，若隸屬度為0，該項可以忽略不寫。

（3）序偶法，例如 ，序偶對的前者是論域中的元素，後者是該元素對應的隸屬度。

（4）向量法，在有限論域的場合，給論域中元素規定一個表達的順序，那么可以將上述序偶法簡寫為隸屬度的向量式，如A= (1,0.5,0.72,0) 。

模糊度

一個模糊集A的模糊度衡量、反映了A的模糊程度，一個直觀的定義是這樣的：

設映射D:F(U) → [0,1] 滿足下述5條性質：

1. 清晰性：D(A) = 0 若且唯若A∈P(U)。（經典集的模糊度恆為0。）
2. 模糊性：D(A) = 1 若且唯若 ∀u∈U有A(u) = 0.5。（隸屬度都為0.5的模糊集最模糊。）
3. 單調性：∀u∈U，若A(u) ≤B(u) ≤ 0.5，或者A(u) ≥B(u) ≥ 0.5，則D(A) ≤D(B)。
4. 對稱性：∀A∈F(U)，有D(A) =D(A)。（補集的模糊度相等。）
5. 可加性：D(A∪B) +D(A∩B)=D(A) +D(B)。

則稱D是定義在F(U) 上的模糊度函式，而D(A) 為模糊集A的模糊度。

可以證明符合上述定義的模糊度是存在的，一個常用的公式（分別針對有限和無限論域）就是

其中p> 0 是參數，稱為 Minkowski 模糊度。特別地，當p= 1 的時候稱為 Hamming 模糊度或 Kaufmann 模糊指標，當p= 2 的時候稱為 Euclid 模糊度。

模糊集的運算

各種運算元

• Zadeh 運算元，max 即為並，min 即為交

• 代數運算元（機率和、代數積）

• 有界運算元

• Einstein 運算元