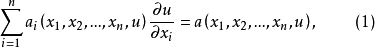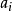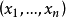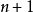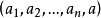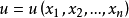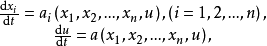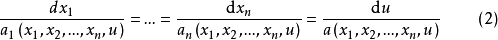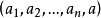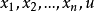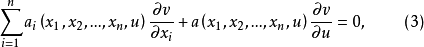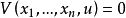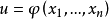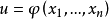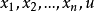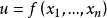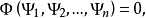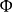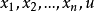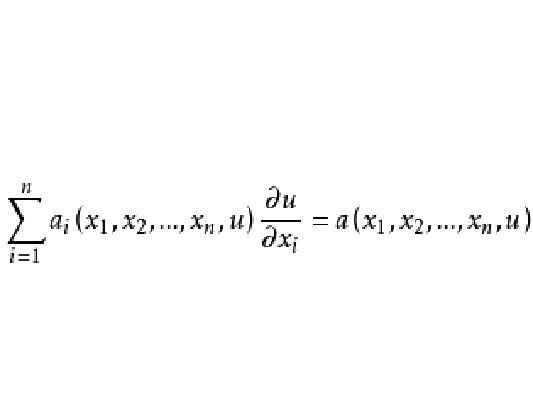一階擬線性偏微分方程

一階擬線性偏微分方程(quasi-linear partial differential equation of first order)是一類特殊的一階非線性偏微分方程，關於未知函式的偏導數是線性的一階非線性偏微分方程稱為一階擬線性偏微分方程。

基本介紹

• 中文名：一階擬線性偏微分方程
• 外文名：quasi-linear partial differential equation of first order
• 所屬學科：數學
• 所屬問題：偏微分方程(一階偏微分方程)
• 相關概念：特徵方程，特徵線，偏導數等

基本介紹

一階擬線性偏微分方程是一類特殊的一階非線性偏微分方程。關於未知函式的偏導數是線性的一階非線性偏微分方程稱為一階擬線性偏微分方程，一階擬線性偏微分方程通常可以寫成下列形狀

其中和為和的已知連續可微函式，

其幾何意義為，在維空間中的每一點給定了一個方向，曲面在該點上的法方向

與方向正交，或者說，曲面在該點與此方向相切。常微分方程組

或

稱為上述一階擬線性偏微分方程的特徵方程。特徵方程的積分曲線，或向量場的積分曲線稱為該一階擬線性偏微分方程的特徵線。

求解問題

假設在變數的維空間的某一區城D，和為其變數的可微函式。

已給變數的任一函式，若此函式對這些變數都有偏導數，且能使方程(1)化為恆等式，則稱此函式為方程(1)的解。和線性方程一樣，可以把此解解釋為空間中的曲面。

讓方程(1) 和下列線性方程

相對應。

定理1設為方程(3) 的解，設方程在變數的區域G決定了某一可微函式，且設在G內，則是方程(1) 的解。

和線性情況不同，在擬線性情況，特徵線不在空間，而在空間，所以這時特徵線另有幾何意義，有下列事實。

定理2每一積分曲面按下述意義由特徵線組成：經過此曲面的每一點可引某一條完全位於其上的特徵線。

為了求解方程(1)，應該按照下列方式進行。組成方程組(線性方程(3)的特徵線方程組)：

(把方程組(4) 的積分曲線，即線性方程(3)的特徵線稱為擬線性方程(1)的特徵線)對此方程組求積分，求出n個獨立的第一積分：

方程(1)的通積分可以這樣寫出：

其中是任意可微函式，這時假設函式是連續可微的，在所研究的變數的變化區域內不變為0。