如果一個方程(組)對於未知函式的所有最高階導數都是線性的,則稱為擬線性方程(組),由最高階導數組成的部分稱為方程的主部,如果擬線性方程主部的各項係數不含未知函式,則稱為半線性方程。
基本介紹
- 中文名:擬線性方程
- 外文名:quasilinear equation
- 所屬學科:數學
- 相關概念:非線性偏微分方程,特徵線等
一階擬線性方程
基本介紹
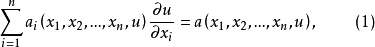


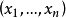

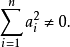
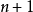
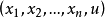
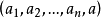
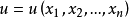

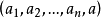
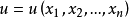
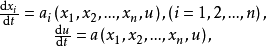
求解問題

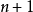
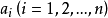


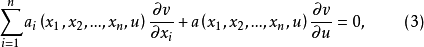









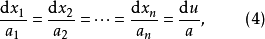

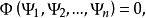
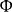
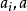

二階擬線性方程


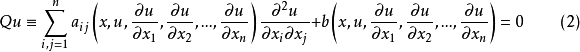

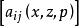
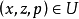


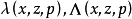
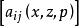
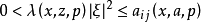


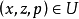
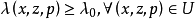

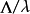



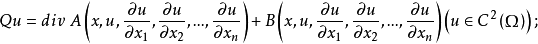
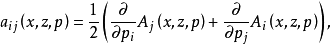

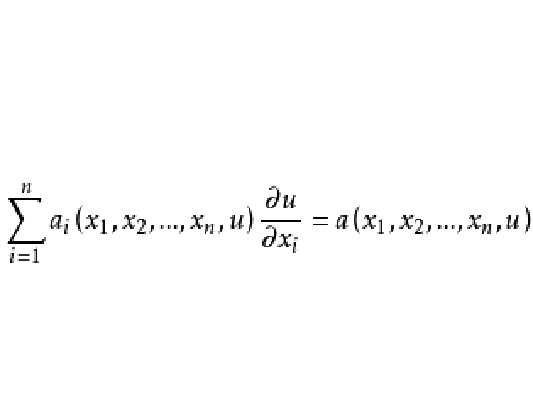
如果一個方程(組)對於未知函式的所有最高階導數都是線性的,則稱為擬線性方程(組),由最高階導數組成的部分稱為方程的主部,如果擬線性方程主部的各項係數不含未知函式,則稱為半線性方程。
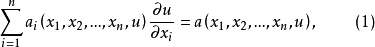


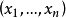

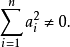
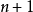
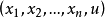
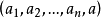
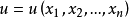

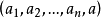
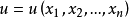
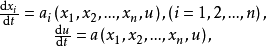

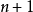
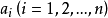


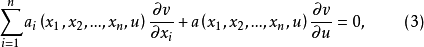









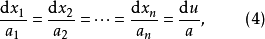

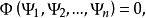
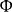
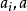



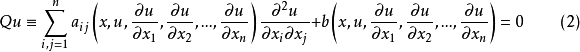

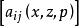
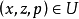


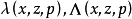
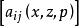
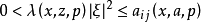


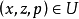
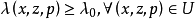

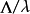



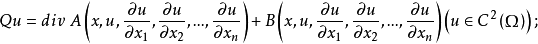
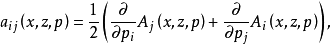

如果一個方程(組)對於未知函式的所有最高階導數都是線性的,則稱為擬線性方程(組),由最高階導數組成的部分稱為方程的主部,如果擬線性方程主部的各項係數不含...
一階擬線性偏微分方程(quasi-linear partial differential equation of first order)是一類特殊的一階非線性偏微分方程,關於未知函式的偏導數是線性的一階非線性偏...
二階擬線性橢圓型方程(quasilinear elliptic equations of second order)是關於二階導數為線性且其係數矩陣為正定的二階非線性偏微分方程,非線性偏微分方程是關於(...
1. 線性和擬線性橢圓型方程 .豆瓣網[引用日期2014-10-25] V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:2次歷史版本 最近更新: 創建者:acrl猜...
《擬線性橢圓型方程的變分方法》是1995年8月1日由華南理工大學出版社出版的圖書,作者是沈堯天。...
二階擬線性退縮拋物方程和擬線性退橢圓方程作者市趙俊寧。由王柔懷、伍卓群教授指導。屬於基礎數學學科。...
可以說,調和方程是最基本,同時也是最重要的線性橢圓型方程。橢圓型偏微分方程非線性 對於非線性方程,也可以定義橢圓型方程。例如,考慮二階實係數擬線性方程...
《擬線性橢圓型方程的軸對稱解》是宣本金1998年寫的一篇論文,屬於基礎數學學科。...... 《擬線性橢圓型方程的軸對稱解》是宣本金1998年寫的一篇論文,屬於基礎數學學...
一階非線性偏微分方程(non-linear partial dif- ferential equation of first order)一階的完全非線 J勝偏微分方程.兩個自變數的一階非線性偏微分方 程的一般...
《奇異擬線性橢圓型方程Dirichlet問題燃燒問題的數學分析》是由張志軍著,陳文〓教授指導的論文。...
關於x與t異性的Sobolev空間Wp2,1的嵌入定理,建立了拋物型方程的Schauder理論,Lp理論,然後與De Giorgi-Nash-Moser估計結合,證明了散度型擬線性拋物型方程解的相當...
第一部分 有界洞型區域內半線性橢圓方程組的正解第二部分 有界洞型區域上一類半線性橢圓型方程的可解性第三章 一類半線性、擬線性橢圓方程(組)邊值問題弱解...
包含近年來出現的最新技巧,並討論線性方程、擬線性方程以及完全非線性方程 Dirichlet問題的可解性;第H部分介紹線性和非線性橢圓型方程組 Dirichlet問題弱解的存在性和...
就稱方程是 中的擬線性橢圓型方程。類似地,可以定義高階擬線性橢圓型方程。 [1] 拉普拉斯運算元推廣 編輯 拉普拉斯運算元可以用一定的方法推廣到非歐幾里德空間,這時...
周毓麟,數學家、套用數學家。1923年2月12日出生於上海,1945年畢業於大同大學數學系。早年從事拓撲學研究,1954年赴莫斯科大學留學,主攻非線性偏微分方程。1957年獲...
在擬線性雙曲型守恆律方面的研究中,運用具間斷右端的常微分方程理論,並且引進“廣義特徵”的概念;在二階擬線性問題研究中,運用退縮拋物方程;尤其是在關於不具凸...
