基本介紹
- 中文名:差分法
- 外文名:difference methods
- 套用學科:數學
- 類別:微分方程數值方法
- 套用:計量經濟學 彈性力學
- 用途:尋求微分方程的近似解
例子
常微分方程
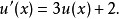
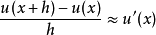
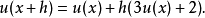
熱傳導方程
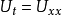
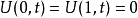
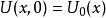
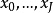
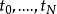
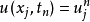
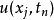
顯式方法
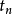

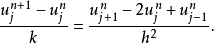
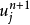
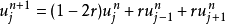
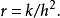
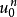
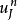
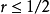
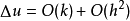
隱式方法
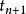
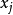
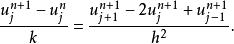
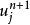
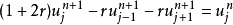
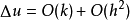
準確度及誤差
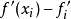
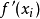
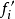
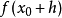
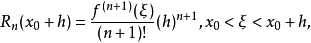
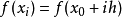
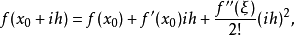
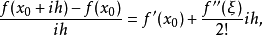
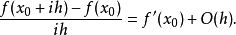

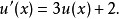
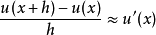
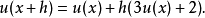
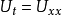
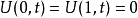
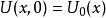
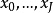
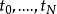
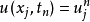
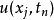
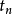

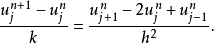
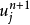
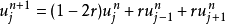
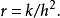
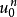
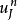
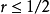
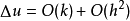
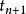
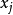
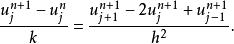
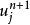
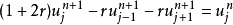
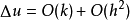
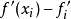
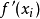
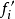
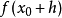
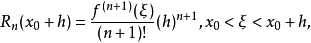
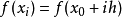
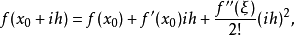
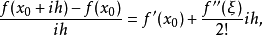
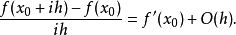
在數學中,差分法(difference methods,簡稱DM),是一種微分方程數值方法,是通過有限差分來近似導數,從而尋求微分方程的近似解。“差分法”是在比較兩個分數大小時,...
有限差分方法(finite difference method)一種求偏微分(或常微分)方程和方程組定解問題的數值解的方法,簡稱差分方法。...
偽距差分法編輯 鎖定 本詞條缺少信息欄、名片圖,補充相關內容使詞條更完整,還能快速升級,趕緊來編輯吧!地面接收機對所有可見衛星測量偽距,並根據星曆數據和已知...
幀間差分法是一種通過對視頻圖像序列中相鄰兩幀作差分運算來獲得運動目標輪廓的方法,它可以很好地適用於存在多個運動目標和攝像機移動的情況。當監控場景中出現...
差分接收機和用戶接收機一樣,通過偽距測量確定自己的位置。把測量確定的位置數據和已知位置數據比較,即得位置校正量x、y、z,通過發射機把這些位置修正信息傳送給...
背景差分法是採用圖像序列中的當前幀和背景參考模型比較來檢測運動物體的一種方法,其性能依賴於所使用的背景建模技術。在基於背景差分方法的運動目標檢測中,背景圖像...
差分法定位 ...... 差分法定點陣圖集 差分法定點陣圖冊 V百科往期回顧 詞條統計 瀏覽次數:次 編輯次數:2次歷史版本 最近更新: 創建者:百科ROBOT...
歐拉有限差分法(Eider finite difference met-hod)一種用有限差分法求泛函 在邊界條件y=ya,y=y。下的極值的方法.其步驟如下:1.將積分區間仁a,司...
《衍生證券與差分法》是2012年出版的圖書,作者是朱友蘭。...... 《衍生證券與差分法(英文)》旨在為讀者提供運用偏微分方程為金融衍生品定價的方法。在第一部分...
1. 科學計算中的偏微分方程有限差分法 .豆瓣[引用日期2019-03-20] 詞條標籤: 文化, 出版物 圖集 科學計算中的偏微分方程有限差分方法圖冊 V百科往期回顧 ...
《科學計算中的偏微分方程有限差分法》是高等教育出版社2006-6-1出版的圖書。...... 《科學計算中的偏微分方程有限差分法》是高等教育出版社2006-6-1出版的圖書...
拉格朗日差分法(Lagrangian difference methods)一類偏微分方程數值解法.指利用拉格朗日坐標,從拉格朗日形式流體力學方程出發求解流體力學問題的差分方法的總稱,簡稱拉格朗日...
歐拉差分法(Eulerian difference methods)一類偏微分方程數值解法,指利用歐拉坐標系,從歐拉形式流體動力學方程出發的求解流體力學問題的差分方法的總稱。...
雙曲型方程差分法(finitedifferencemethodsofhyperbolicequation)數值求解雙曲型偏微分方程初值問題和初邊值問題的主要方法.它的基本步驟和研究內容見“偏微分方程初值...
偏微分方程初值問題差分法是一種求解偏微分方程初值問題和初邊值問題的主要數值方法。...
差分法的思想和做法是,把定解區域剖分為格線,在格線結點上以差商代替微商或用某種插值方式,把微分方程化為包含有限個未知數的差分方程組。差分法直觀、簡易、能...
《拋物型方程差分方法引論》是科學出版社出版的圖書。...... 1??8 追趕法的幾種不同形式 附錄:嵌入定理的差分模擬 第二章 統一差分格式 2??1 變係數定常...
《跨音速定常勢流的混合差分法》是一本理科、工程技術類專用圖書。...... 《跨音速定常勢流的混合差分法》是一本理科、工程技術類專用圖書。《跨音速定常勢流...
《MATLAB模擬的電磁學時域有限差分法》是出版的一本圖書...... 《MATLAB模擬的電磁學時域有限差分法》介紹了近年來在電磁領域內發展較快的時域有限差分法(FDTD)的...
