狄利克雷邊界條件,常微分方程的“第一類邊界條件”,指定微分方程的解在邊界處的值。
基本介紹
簡介
在常微分方程情況下




在偏微分方程情況下
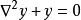

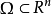



狄利克雷邊界條件,常微分方程的“第一類邊界條件”,指定微分方程的解在邊界處的值。




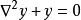

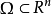


狄利克雷邊界條件,常微分方程的“第一類邊界條件”,指定微分方程的解在邊界處的值。...
在數學中,狄利克雷邊界條件,為常微分方程的“第一類邊界條件”,指定微分方程的解在邊界處的值。求出這樣的方程的解的問題被稱為狄利克雷問題。狄利克雷問題(...
本質邊界條件即狄里克雷邊界條件,又稱為第一類邊界條件,指預先對容許函式所加的邊界條件。...
數學中,經典狄利克雷問題(classical Dirichlet problem)是尋找一個函式,使其為給定區域內一個指定的偏微分方程(PDE)的解,且在邊界上取預定值。...
狄利克雷區域是一類特殊區域。對於狄利克雷問題是可解的域D,稱為狄利克雷區域。...... 在數學中,狄利克雷邊界條件,為常微分方程的“第一類邊界條件”,指定微分...
狄利克雷條件 半無限大物體在導熱方向上,當其邊界溫度一定為第一類。數學描述為:T(x,0) =f(x);T(0,t) = Ts第一類邊界是給定邊界上待求變數的分布第...
廣義狄利克雷問題(generalized Dirichlet problem)是經典狄利克雷問題通過適當放鬆邊界值要求進行的推廣。而經典狄利克雷問題也叫做第一邊值問題,是經典位勢論中三大...
邊值問題是定解問題之一,只有邊界條件的定解問題稱為邊值問題。二階偏微分方程(組)一般有三種邊值問題:第一邊值問題又稱狄利克雷問題,它的邊界條件是給出未知...
可以使用其他邊界條件來描述問題:狄利克雷邊界條件指定邊界上的解本身(與其導數相反)的值,而柯西邊界條件,混合邊界條件和羅賓邊界條件都是不同的諾伊曼和狄利克雷邊界...
為了解泊松方程我們需要更多的信息,比如狄利克雷邊界條件:其中 為有界開集。這種情況下利用基礎函式構建泊松方程的解,拉普拉斯方程的基礎函式為:...
這就意味著,該方程的解的梯度是唯一確定的,若且唯若如下條件成立使得上式成立的邊值條件包括:狄利克雷邊界條件: 在曲面邊界有定義。 因此 。於是,在邊界任意...
在弦論中,D-膜是一種物體可以讓開弦的端點以狄利克雷邊界條件固定的地方。D-模是在1989年由Dai, Leigh和約瑟夫·泡耳欽斯基發現,另外較罕為人知的是,切赫·荷...
都有定義,且具有給定的邊界條件嗎?狄利克雷原理提供了肯定的答案。只要確立了u的存在,全純函式的柯西-黎曼方程便允許了我們求出 (這個論證依賴於 是單連通的假設...
若是二階的常微分方程,也可能會指定函式在二個特定點的值,此時的問題即為邊界值問題。若邊界條件指定二點數值,稱為狄利克雷邊界條件(第一類邊值條件),此外也有...
有兩類基本的邊界條件:給定邊界面上各點的電勢,叫做狄利克雷邊界條件;給定邊界面上各點的自由電荷,叫做諾埃曼邊界條件。 邊界幾何形狀較簡單區域的靜電場可求得...
緊湊的維度對所有場施加了特定的邊界條件,例如在周期性維度的情況下的周期性邊界條件,並且在其他情況下通常為諾伊曼邊界條件或狄利克雷邊界條件。 [1] 現在假設緊湊...
格林還研究了弦論中的狄利克雷邊界條件,他的結果導致了D膜和瞬子解的提出。麥可·格林獲得榮譽 編輯 格林已發表150餘篇研究論文,獲得過眾多獎勵和榮譽。1987年...
例如,在狄利克雷邊界條件下拉普拉斯方程的中,F 是一個區域 R 上的拉普拉斯運算元,G 是將 y 限制於 R 的邊界上的運算元,z 是 y 在 R 的邊界上要求滿足的函式...
考慮正規化的一維熱傳導方程式,為齊次的狄利克雷邊界條件(邊界條件)(初始條件)對此問題求數值解的一種方式是用差分去近似所有的導數,可以將空間分割為 ,將時間也...
附加第一類和第二類邊界條件的問題分別稱為狄利克雷問題和馮·諾伊曼問題;有些問題在邊界不同區段滿足不同類的邊界條件,稱為混合邊值問題。 橢圓型邊值問題的...
例如滿足狄利克雷邊界條件的一維熱傳導問題,其解(時間的函式)可以寫成許多不同頻率之正弦函式的線性組合,而這也讓它的解很彈性、具有很大的變化空間。通常我們可以...
邊值問題(boundary value problem)是定解問題之一,只有邊界條件的定解問題稱為邊值問題。二階偏微分方程(組)一般有三種邊值問題:第一邊值問題又稱狄利克雷問題,...
球的狄利克雷問題的解3.7 邊值問題解的唯一性和對邊界條件的連續依賴性3.8 導數的先驗估計.解析性3.9 劉維爾定理和弗拉格門-林德勒夫定理3.10 調和函式的孤立...
