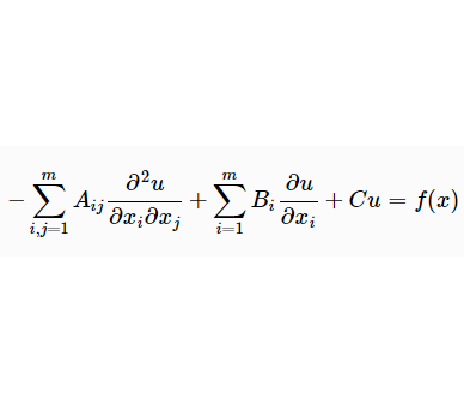斜微商問題

斜微商問題(oblique derivative problem)是求解滿足斜微商邊界條件的橢圓型方程的解的問題，又稱諾伊曼邊值問題、第二邊值問題，它的邊界條件是給出未知函式關於區域邊界的法嚮導數或非切嚮導數。

基本介紹

• 中文名：斜微商問題
• 外文名：oblique derivative problem
• 別稱：諾伊曼邊值問題、第二邊值問題
• 所屬學科：數學
• 所屬問題：偏微分方程(偏微分方程基本解法)
• 相關概念：斜微商邊界條件、橢圓型方程等

簡介

斜微商問題是求解滿足斜微商邊界條件的橢圓型方程的解的問題，形如

的邊界條件稱為斜微商邊界條件，若向量的法向分量在上非零，則稱上述條件為正則斜微商邊界條件。

唯一性定理

對於斜微商問題成立下面的唯一性定理：

1) 如果區域是有限的，井且而且這些函式中至少有一個不恆等於零，則斜微商問題的解不會多於一個；

2) 如果是無限的，而解服從條件，則解是唯一的；

3) 如果區域有限，，則斜微商問題的兩個解之間只能相差一個常數項。

若唯一性定理成立，則斜導數同題是可解的；若唯一性定理不成立，則齊次問題的解的個數是有限的，而非齊次方程若且唯若函式與方程(6)（見下文）的共軛齊次方程的全體解(個數也是有限的)正交時才可解。

問題分析

考察橢圓型方程

它的左邊部分的係數足夠多次連續可微，關於方程(1)的斜微商問題是按下面的方式提出的。假設是空間中為曲面所包圍的區域。對上的每一點，聯繫一個方向，要求找方程(1)的積分，滿足邊界條件

其中是給定在上的函式。

我們只限於討論這樣的情形，即為足夠光滑的閉曲面，而在曲面的任一點上，方向與其外法線成銳角且為點的足夠光滑的函式。

我們用下面的方式來解決這問題。取，這是可以做到的，只要從未知函式中減去具有密度的體位勢。其次，假設曲面是這樣的，它對於任一滿足已知光滑性條件的方程

的解可以表示為下面形式的單層位勢

而且這種表示是唯一的，把表示式(4)代入邊界條件(2)，得到了未知函式的奇異積分方程，我們來尋求這個方程的形式。

套用通常的位勢理論的方法，不難得到公式

這個公式首先是由G.Giraud得到的；負號和正號對應於曲面的內極限和外極限，其次，

是曲面的外法向，關於的方程具有形式

可以證明，只要方向與到處不相切，則方程(6)的符號到處不為零。

對於方程(6)，Fredholm定理是正確的，所以，若唯一性定理成立，則斜導數同題是可解的；若唯一性定理不成立，則齊次問題的解的個數是有限的，而非齊次方程若且唯若函式與方程(6)的共軛齊次方程的全體解(個數也是有限的)正交時才可解（更多分析見相應參考資料）。

邊值問題

邊值問題(boundary value problem)是定解問題之一，只有邊界條件的定解問題稱為邊值問題。二階偏微分方程(組)一般有三種邊值問題：第一邊值問題又稱狄利克雷問題，它的邊界條件是給出未知函式本身在邊界上的值；第二邊值問題又稱諾伊曼邊值問題或斜微商問題，它的邊界條件是給出未知函式關於區域邊界的法嚮導數或非切嚮導數；第三邊值問題又稱魯賓問題，它的邊界條件是給出未知函式及其非切嚮導數的組合。