維度減化（英語：Dimensional reduction）是緊化理論中緊緻化的維度的大小變為零時的臨界情況。在物理學中，通過將所有的場獨立存在於額外維度D中，時空維數D的理論能夠被較少數量的額外維度D重新定義。
基本介紹
- 中文名：維度減化
- 外文名：Dimensional reduction
- 學科：物理
維度減化詳解,背景,
維度減化詳解
例如，考慮一個周期性的緊湊的維度的L時期。讓x成為沿著這條維度的坐標。任何場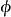
可以被描述為以下單元的總和：
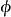
An作為一個常數。根據量子力學，這一單元具有沿著x軸的動量nh/L，在那裡h是普朗克常數。因此，當L達到0時，這個動量達到了無限大，能量也一樣，除非n=0。然而n=0提供了一個關於x恆定的場。因此在這個場的限制下，並在有限的能量下， 
將不依賴於x。
這種說法進行了概括。緊湊的維度對所有場施加了特定的邊界條件，例如在周期性維度的情況下的周期性邊界條件，並且在其他情況下通常為諾伊曼邊界條件或狄利克雷邊界條件。現在假設緊湊的維度的尺度是L；那么沿這個維度的梯度的可能的特徵值是1/L的整數或半整數倍（取決於精確的邊界條件）。在量子力學中，這個特徵值是場的動量，因此與其能量有關。當L→0時，除零之外的所有特徵值都到無窮大，而能量也是如此。因此，在這個極限情況下，在有限能量的情況下，零是唯一可能的沿著緊湊尺寸的梯度下的特徵值，這意味著沒有任何東西依賴於這個維度。
背景
將五維時空分開成四維的愛因斯坦方程式以及麥克斯韋方程組是首先由古納爾·諾德斯特諾姆於1914年所發現，出現在他的重力理論內文中，但隨後就被世人遺忘。在1926年，奧斯卡·克萊因（Oskar Klein）提議了第四個空間維度捲曲成一個半徑非常小的圓，所以粒子沿著這個軸移動很短的距離，就會回到起始點。粒子在回到起始點前所能行進的距離則稱作是該維度的大小。這個額外維度（extra dimension）是一個緊集，而時空具有緊緻維度的現象則稱作是緊化。
第五維度捲曲成圓，構成了最早的高維宇宙模型。此模型僅多出現了一個額外維度。
現代幾何學中，額外的第五維度可以被理解為圓群U(1)，而基本上，電磁學可以用在纖維叢上規範群U（1）的規範場論來詮釋。一旦這樣的幾何詮釋能被理解，則將U（1）換成廣義的李群就顯得容易而直觀。這樣的推廣常稱作是楊-米爾斯理論。若要提到兩者的差異，則可說楊–米爾斯理論是在平坦時空的場合處理，而卡魯扎-克萊因理論則是在更具一般性的彎曲時空中處理。卡魯扎-克萊因理論的底空間不一定是四維時空，而可以是任何的（偽）黎曼流形，或者甚至是超對稱流形、軌形或非交換空間。
